Author: Jason Brownlee
Multilayer Perceptrons, or MLPs for short, can be applied to time series forecasting.
A challenge with using MLPs for time series forecasting is in the preparation of the data. Specifically, lag observations must be flattened into feature vectors.
In this tutorial, you will discover how to develop a suite of MLP models for a range of standard time series forecasting problems.
The objective of this tutorial is to provide standalone examples of each model on each type of time series problem as a template that you can copy and adapt for your specific time series forecasting problem.
In this tutorial, you will discover how to develop a suite of Multilayer Perceptron models for a range of standard time series forecasting problems.
After completing this tutorial, you will know:
- How to develop MLP models for univariate time series forecasting.
- How to develop MLP models for multivariate time series forecasting.
- How to develop MLP models for multi-step time series forecasting.
Let’s get started.

How to Develop Multilayer Perceptron Models for Time Series Forecasting
Photo by Bureau of Land Management, some rights reserved.
Tutorial Overview
This tutorial is divided into four parts; they are:
- Univariate MLP Models
- Multivariate MLP Models
- Multi-Step MLP Models
- Multivariate Multi-Step MLP Models
Univariate MLP Models
Multilayer Perceptrons, or MLPs for short, can be used to model univariate time series forecasting problems.
Univariate time series are a dataset comprised of a single series of observations with a temporal ordering and a model is required to learn from the series of past observations to predict the next value in the sequence.
This section is divided into two parts; they are:
- Data Preparation
- MLP Model
Data Preparation
Before a univariate series can be modeled, it must be prepared.
The MLP model will learn a function that maps a sequence of past observations as input to an output observation. As such, the sequence of observations must be transformed into multiple examples from which the model can learn.
Consider a given univariate sequence:
[10, 20, 30, 40, 50, 60, 70, 80, 90]
We can divide the sequence into multiple input/output patterns called samples, where three time steps are used as input and one time step is used as output for the one-step prediction that is being learned.
X, y 10, 20, 30 40 20, 30, 40 50 30, 40, 50 60 ...
The split_sequence() function below implements this behavior and will split a given univariate sequence into multiple samples where each sample has a specified number of time steps and the output is a single time step.
# split a univariate sequence into samples def split_sequence(sequence, n_steps): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the sequence if end_ix > len(sequence)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y)
We can demonstrate this function on our small contrived dataset above.
The complete example is listed below.
# univariate data preparation from numpy import array # split a univariate sequence into samples def split_sequence(sequence, n_steps): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the sequence if end_ix > len(sequence)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90] # choose a number of time steps n_steps = 3 # split into samples X, y = split_sequence(raw_seq, n_steps) # summarize the data for i in range(len(X)): print(X[i], y[i])
Running the example splits the univariate series into six samples where each sample has three input time steps and one output time step.
[10 20 30] 40 [20 30 40] 50 [30 40 50] 60 [40 50 60] 70 [50 60 70] 80 [60 70 80] 90
Now that we know how to prepare a univariate series for modeling, let’s look at developing an MLP model that can learn the mapping of inputs to outputs.
Need help with Deep Learning for Time Series?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
MLP Model
A simple MLP model has a single hidden layer of nodes, and an output layer used to make a prediction.
We can define an MLP for univariate time series forecasting as follows.
# define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_steps)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse')
Important in the definition is the shape of the input; that is what the model expects as input for each sample in terms of the number of time steps.
The number of time steps as input is the number we chose when preparing our dataset as an argument to the split_sequence() function.
The input dimension for each sample is specified in the input_dim argument on the definition of first hidden layer. Technically, the model will view each time step as a separate feature instead of separate time steps.
We almost always have multiple samples, therefore, the model will expect the input component of training data to have the dimensions or shape:
[samples, features]
Our split_sequence() function in the previous section outputs the X with the shape [samples, features] ready to use for modeling.
The model is fit using the efficient Adam version of stochastic gradient descent and optimized using the mean squared error, or ‘mse‘, loss function.
Once the model is defined, we can fit it on the training dataset.
# fit model model.fit(X, y, epochs=2000, verbose=0)
After the model is fit, we can use it to make a prediction.
We can predict the next value in the sequence by providing the input:
[70, 80, 90]
And expecting the model to predict something like:
[100]
The model expects the input shape to be two-dimensional with [samples, features], therefore, we must reshape the single input sample before making the prediction, e.g with the shape [1, 3] for 1 sample and 3 time steps used as input features.
# demonstrate prediction x_input = array([70, 80, 90]) x_input = x_input.reshape((1, n_steps)) yhat = model.predict(x_input, verbose=0)
We can tie all of this together and demonstrate how to develop an MLP for univariate time series forecasting and make a single prediction.
# univariate mlp example from numpy import array from keras.models import Sequential from keras.layers import Dense # split a univariate sequence into samples def split_sequence(sequence, n_steps): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the sequence if end_ix > len(sequence)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90] # choose a number of time steps n_steps = 3 # split into samples X, y = split_sequence(raw_seq, n_steps) # define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_steps)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse') # fit model model.fit(X, y, epochs=2000, verbose=0) # demonstrate prediction x_input = array([70, 80, 90]) x_input = x_input.reshape((1, n_steps)) yhat = model.predict(x_input, verbose=0) print(yhat)
Running the example prepares the data, fits the model, and makes a prediction.
Your results may vary given the stochastic nature of the algorithm; try running the example a few times.
We can see that the model predicts the next value in the sequence.
[[100.0109]]
Multivariate MLP Models
Multivariate time series data means data where there is more than one observation for each time step.
There are two main models that we may require with multivariate time series data; they are:
- Multiple Input Series.
- Multiple Parallel Series.
Let’s take a look at each in turn.
Multiple Input Series
A problem may have two or more parallel input time series and an output time series that is dependent on the input time series.
The input time series are parallel because each series has an observation at the same time step.
We can demonstrate this with a simple example of two parallel input time series where the output series is the simple addition of the input series.
# define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
We can reshape these three arrays of data as a single dataset where each row is a time step and each column is a separate time series. This is a standard way of storing parallel time series in a CSV file.
# convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq))
The complete example is listed below.
# multivariate data preparation from numpy import array from numpy import hstack # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) print(dataset)
Running the example prints the dataset with one row per time step and one column for each of the two input and one output parallel time series.
[[ 10 15 25] [ 20 25 45] [ 30 35 65] [ 40 45 85] [ 50 55 105] [ 60 65 125] [ 70 75 145] [ 80 85 165] [ 90 95 185]]
As with the univariate time series, we must structure these data into samples with input and output samples.
We need to split the data into samples maintaining the order of observations across the two input sequences.
If we chose three input time steps, then the first sample would look as follows:
Input:
10, 15 20, 25 30, 35
Output:
65
That is, the first three time steps of each parallel series are provided as input to the model and the model associates this with the value in the output series at the third time step, in this case 65.
We can see that, in transforming the time series into input/output samples to train the model, that we will have to discard some values from the output time series where we do not have values in the input time series at prior time steps. In turn, the choice of the size of the number of input time steps will have an important effect on how much of the training data is used.
We can define a function named split_sequences() that will take a dataset as we have defined it with rows for time steps and columns for parallel series and return input/output samples.
# split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1] X.append(seq_x) y.append(seq_y) return array(X), array(y)
We can test this function on our dataset using three time steps for each input time series as input.
The complete example is listed below.
# multivariate data preparation from numpy import array from numpy import hstack # split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps = 3 # convert into input/output X, y = split_sequences(dataset, n_steps) print(X.shape, y.shape) # summarize the data for i in range(len(X)): print(X[i], y[i])
Running the example first prints the shape of the X and y components.
We can see that the X component has a three-dimensional structure.
The first dimension is the number of samples, in this case 7. The second dimension is the number of time steps per sample, in this case 3, the value specified to the function. Finally, the last dimension specifies the number of parallel time series or the number of variables, in this case 2 for the two parallel series.
We can then see that the input and output for each sample is printed, showing the three time steps for each of the two input series and the associated output for each sample.
(7, 3, 2) (7,) [[10 15] [20 25] [30 35]] 65 [[20 25] [30 35] [40 45]] 85 [[30 35] [40 45] [50 55]] 105 [[40 45] [50 55] [60 65]] 125 [[50 55] [60 65] [70 75]] 145 [[60 65] [70 75] [80 85]] 165 [[70 75] [80 85] [90 95]] 185
Before we can fit an MLP on this data, we must flatten the shape of the input samples.
MLPs require that the shape of the input portion of each sample is a vector. With a multivariate input, we will have multiple vectors, one for each time step.
We can flatten the temporal structure of each input sample, so that:
[[10 15] [20 25] [30 35]]
Becomes:
[10, 15, 20, 25, 30, 35]
First, we can calculate the length of each input vector as the number of time steps multiplied by the number of features or time series. We can then use this vector size to reshape the input.
# flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input))
We can now define an MLP model for the multivariate input where the vector length is used for the input dimension argument.
# define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_input)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse')
When making a prediction, the model expects three time steps for two input time series.
We can predict the next value in the output series proving the input values of:
80, 85 90, 95 100, 105
The shape of the 1 sample with 3 time steps and 2 variables would be [1, 3, 2]. We must again reshape this to be 1 sample with a vector of 6 elements or [1, 6]
We would expect the next value in the sequence to be 100 + 105 or 205.
# demonstrate prediction x_input = array([[80, 85], [90, 95], [100, 105]]) x_input = x_input.reshape((1, n_input)) yhat = model.predict(x_input, verbose=0)
The complete example is listed below.
# multivariate mlp example from numpy import array from numpy import hstack from keras.models import Sequential from keras.layers import Dense # split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps = 3 # convert into input/output X, y = split_sequences(dataset, n_steps) # flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input)) # define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_input)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse') # fit model model.fit(X, y, epochs=2000, verbose=0) # demonstrate prediction x_input = array([[80, 85], [90, 95], [100, 105]]) x_input = x_input.reshape((1, n_input)) yhat = model.predict(x_input, verbose=0) print(yhat)
Running the example prepares the data, fits the model, and makes a prediction.
[[205.04436]]
There is another more elaborate way to model the problem.
Each input series can be handled by a separate MLP and the output of each of these submodels can be combined before a prediction is made for the output sequence.
We can refer to this as a multi-headed input MLP model. It may offer more flexibility or better performance depending on the specifics of the problem that are being modeled.
This type of model can be defined in Keras using the Keras functional API.
First, we can define the first input model as an MLP with an input layer that expects vectors with n_steps features.
# first input model visible1 = Input(shape=(n_steps,)) dense1 = Dense(100, activation='relu')(visible1)
We can define the second input submodel in the same way.
# second input model visible2 = Input(shape=(n_steps,)) dense2 = Dense(100, activation='relu')(visible2)
Now that both input submodels have been defined, we can merge the output from each model into one long vector, which can be interpreted before making a prediction for the output sequence.
# merge input models merge = concatenate([dense1, dense2]) output = Dense(1)(merge)
We can then tie the inputs and outputs together.
model = Model(inputs=[visible1, visible2], outputs=output)
The image below provides a schematic for how this model looks, including the shape of the inputs and outputs of each layer.
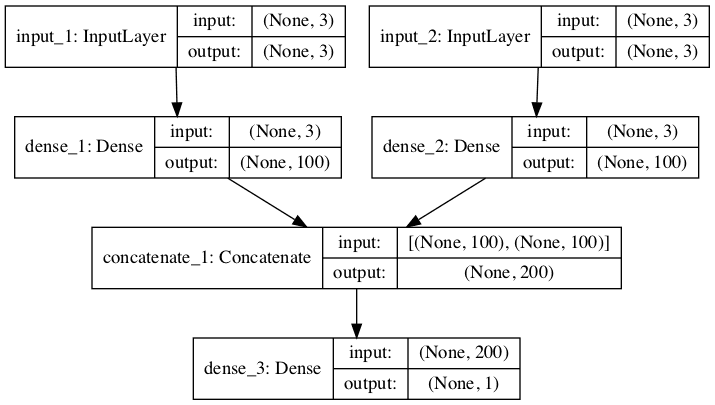
Plot of Multi-Headed MLP for Multivariate Time Series Forecasting
This model requires input to be provided as a list of two elements, where each element in the list contains data for one of the submodels.
In order to achieve this, we can split the 3D input data into two separate arrays of input data: that is from one array with the shape [7, 3, 2] to two 2D arrays with the shape [7, 3]
# separate input data X1 = X[:, :, 0] X2 = X[:, :, 1]
These data can then be provided in order to fit the model.
# fit model model.fit([X1, X2], y, epochs=2000, verbose=0)
Similarly, we must prepare the data for a single sample as two separate two-dimensional arrays when making a single one-step prediction.
x_input = array([[80, 85], [90, 95], [100, 105]]) x1 = x_input[:, 0].reshape((1, n_steps)) x2 = x_input[:, 1].reshape((1, n_steps))
We can tie all of this together; the complete example is listed below.
# multivariate mlp example from numpy import array from numpy import hstack from keras.models import Model from keras.layers import Input from keras.layers import Dense from keras.layers.merge import concatenate # split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1, -1] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps = 3 # convert into input/output X, y = split_sequences(dataset, n_steps) # separate input data X1 = X[:, :, 0] X2 = X[:, :, 1] # first input model visible1 = Input(shape=(n_steps,)) dense1 = Dense(100, activation='relu')(visible1) # second input model visible2 = Input(shape=(n_steps,)) dense2 = Dense(100, activation='relu')(visible2) # merge input models merge = concatenate([dense1, dense2]) output = Dense(1)(merge) model = Model(inputs=[visible1, visible2], outputs=output) model.compile(optimizer='adam', loss='mse') # fit model model.fit([X1, X2], y, epochs=2000, verbose=0) # demonstrate prediction x_input = array([[80, 85], [90, 95], [100, 105]]) x1 = x_input[:, 0].reshape((1, n_steps)) x2 = x_input[:, 1].reshape((1, n_steps)) yhat = model.predict([x1, x2], verbose=0) print(yhat)
Running the example prepares the data, fits the model, and makes a prediction.
[[206.05022]]
Multiple Parallel Series
An alternate time series problem is the case where there are multiple parallel time series and a value must be predicted for each.
For example, given the data from the previous section:
[[ 10 15 25] [ 20 25 45] [ 30 35 65] [ 40 45 85] [ 50 55 105] [ 60 65 125] [ 70 75 145] [ 80 85 165] [ 90 95 185]]
We may want to predict the value for each of the three time series for the next time step.
This might be referred to as multivariate forecasting.
Again, the data must be split into input/output samples in order to train a model.
The first sample of this dataset would be:
Input:
10, 15, 25 20, 25, 45 30, 35, 65
Output:
40, 45, 85
The split_sequences() function below will split multiple parallel time series with rows for time steps and one series per column into the required input/output shape.
# split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :] X.append(seq_x) y.append(seq_y) return array(X), array(y)
We can demonstrate this on the contrived problem; the complete example is listed below.
# multivariate output data prep from numpy import array from numpy import hstack # split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps = 3 # convert into input/output X, y = split_sequences(dataset, n_steps) print(X.shape, y.shape) # summarize the data for i in range(len(X)): print(X[i], y[i])
Running the example first prints the shape of the prepared X and y components.
The shape of X is three-dimensional, including the number of samples (6), the number of time steps chosen per sample (3), and the number of parallel time series or features (3).
The shape of y is two-dimensional as we might expect for the number of samples (6) and the number of time variables per sample to be predicted (3).
Then, each of the samples is printed showing the input and output components of each sample.
(6, 3, 3) (6, 3) [[10 15 25] [20 25 45] [30 35 65]] [40 45 85] [[20 25 45] [30 35 65] [40 45 85]] [ 50 55 105] [[ 30 35 65] [ 40 45 85] [ 50 55 105]] [ 60 65 125] [[ 40 45 85] [ 50 55 105] [ 60 65 125]] [ 70 75 145] [[ 50 55 105] [ 60 65 125] [ 70 75 145]] [ 80 85 165] [[ 60 65 125] [ 70 75 145] [ 80 85 165]] [ 90 95 185]
We are now ready to fit an MLP model on this data.
As with the previous case of multivariate input, we must flatten the three dimensional structure of the input data samples to a two dimensional structure of [samples, features], where lag observations are treated as features by the model.
# flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input))
The model output will be a vector, with one element for each of the three different time series.
n_output = y.shape[1]
We can now define our model, using the flattened vector length for the input layer and the number of time series as the vector length when making a prediction.
# define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_input)) model.add(Dense(n_output)) model.compile(optimizer='adam', loss='mse')
We can predict the next value in each of the three parallel series by providing an input of three time steps for each series.
70, 75, 145 80, 85, 165 90, 95, 185
The shape of the input for making a single prediction must be 1 sample, 3 time steps and 3 features, or [1, 3, 3]. Again, we can flatten this to [1, 6] to meet the expectations of the model.
We would expect the vector output to be:
[100, 105, 205]
# demonstrate prediction x_input = array([[70,75,145], [80,85,165], [90,95,185]]) x_input = x_input.reshape((1, n_input)) yhat = model.predict(x_input, verbose=0)
We can tie all of this together and demonstrate an MLP for multivariate output time series forecasting below.
# multivariate output mlp example from numpy import array from numpy import hstack from keras.models import Sequential from keras.layers import Dense # split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps = 3 # convert into input/output X, y = split_sequences(dataset, n_steps) # flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input)) n_output = y.shape[1] # define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_input)) model.add(Dense(n_output)) model.compile(optimizer='adam', loss='mse') # fit model model.fit(X, y, epochs=2000, verbose=0) # demonstrate prediction x_input = array([[70,75,145], [80,85,165], [90,95,185]]) x_input = x_input.reshape((1, n_input)) yhat = model.predict(x_input, verbose=0) print(yhat)
Running the example prepares the data, fits the model, and makes a prediction.
[[100.95039 107.541306 206.81033 ]]
As with multiple input series, there is another, more elaborate way to model the problem.
Each output series can be handled by a separate output MLP model.
We can refer to this as a multi-output MLP model. It may offer more flexibility or better performance depending on the specifics of the problem that is being modeled.
This type of model can be defined in Keras using the Keras functional API.
First, we can define the input model as an MLP with an input layer that expects flattened feature vectors.
# define model visible = Input(shape=(n_input,)) dense = Dense(100, activation='relu')(visible)
We can then define one output layer for each of the three series that we wish to forecast, where each output submodel will forecast a single time step.
# define output 1 output1 = Dense(1)(dense) # define output 2 output2 = Dense(1)(dense) # define output 2 output3 = Dense(1)(dense)
We can then tie the input and output layers together into a single model.
# tie together model = Model(inputs=visible, outputs=[output1, output2, output3]) model.compile(optimizer='adam', loss='mse')
To make the model architecture clear, the schematic below clearly shows the three separate output layers of the model and the input and output shapes of each layer.
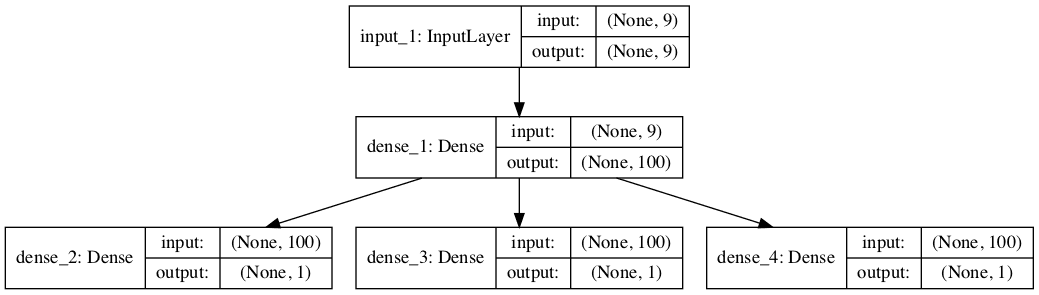
Plot of Multi-Output MLP for Multivariate Time Series Forecasting
When training the model, it will require three separate output arrays per sample.
We can achieve this by converting the output training data that has the shape [7, 3] to three arrays with the shape [7, 1].
# separate output y1 = y[:, 0].reshape((y.shape[0], 1)) y2 = y[:, 1].reshape((y.shape[0], 1)) y3 = y[:, 2].reshape((y.shape[0], 1))
These arrays can be provided to the model during training.
# fit model model.fit(X, [y1,y2,y3], epochs=2000, verbose=0)
Tying all of this together, the complete example is listed below.
# multivariate output mlp example from numpy import array from numpy import hstack from keras.models import Model from keras.layers import Input from keras.layers import Dense # split a multivariate sequence into samples def split_sequences(sequences, n_steps): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the dataset if end_ix > len(sequences)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps = 3 # convert into input/output X, y = split_sequences(dataset, n_steps) # flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input)) # separate output y1 = y[:, 0].reshape((y.shape[0], 1)) y2 = y[:, 1].reshape((y.shape[0], 1)) y3 = y[:, 2].reshape((y.shape[0], 1)) # define model visible = Input(shape=(n_input,)) dense = Dense(100, activation='relu')(visible) # define output 1 output1 = Dense(1)(dense) # define output 2 output2 = Dense(1)(dense) # define output 2 output3 = Dense(1)(dense) # tie together model = Model(inputs=visible, outputs=[output1, output2, output3]) model.compile(optimizer='adam', loss='mse') # fit model model.fit(X, [y1,y2,y3], epochs=2000, verbose=0) # demonstrate prediction x_input = array([[70,75,145], [80,85,165], [90,95,185]]) x_input = x_input.reshape((1, n_input)) yhat = model.predict(x_input, verbose=0) print(yhat)
Running the example prepares the data, fits the model, and makes a prediction.
[array([[100.86121]], dtype=float32), array([[105.14738]], dtype=float32), array([[205.97507]], dtype=float32)]
Multi-Step MLP Models
In practice, there is little difference to the MLP model in predicting a vector output that represents different output variables (as in the previous example) or a vector output that represents multiple time steps of one variable.
Nevertheless, there are subtle and important differences in the way the training data is prepared. In this section, we will demonstrate the case of developing a multi-step forecast model using a vector model.
Before we look at the specifics of the model, let’s first look at the preparation of data for multi-step forecasting.
Data Preparation
As with one-step forecasting, a time series used for multi-step time series forecasting must be split into samples with input and output components.
Both the input and output components will be comprised of multiple time steps and may or may not have the same number of steps.
For example, given the univariate time series:
[10, 20, 30, 40, 50, 60, 70, 80, 90]
We could use the last three time steps as input and forecast the next two time steps.
The first sample would look as follows:
Input:
[10, 20, 30]
Output:
[40, 50]
The split_sequence() function below implements this behavior and will split a given univariate time series into samples with a specified number of input and output time steps.
# split a univariate sequence into samples def split_sequence(sequence, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out # check if we are beyond the sequence if out_end_ix > len(sequence): break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y)
We can demonstrate this function on the small contrived dataset.
The complete example is listed below.
# multi-step data preparation from numpy import array # split a univariate sequence into samples def split_sequence(sequence, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out # check if we are beyond the sequence if out_end_ix > len(sequence): break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90] # choose a number of time steps n_steps_in, n_steps_out = 3, 2 # split into samples X, y = split_sequence(raw_seq, n_steps_in, n_steps_out) # summarize the data for i in range(len(X)): print(X[i], y[i])
Running the example splits the univariate series into input and output time steps and prints the input and output components of each.
[10 20 30] [40 50] [20 30 40] [50 60] [30 40 50] [60 70] [40 50 60] [70 80] [50 60 70] [80 90]
Now that we know how to prepare data for multi-step forecasting, let’s look at an MLP model that can learn this mapping.
Vector Output Model
The MLP can output a vector directly that can be interpreted as a multi-step forecast.
This approach was seen in the previous section were one time step of each output time series was forecasted as a vector.
With the number of input and output steps specified in the n_steps_in and n_steps_out variables, we can define a multi-step time-series forecasting model.
# define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_steps_in)) model.add(Dense(n_steps_out)) model.compile(optimizer='adam', loss='mse')
The model can make a prediction for a single sample. We can predict the next two steps beyond the end of the dataset by providing the input:
[70, 80, 90]
We would expect the predicted output to be:
[100, 110]
As expected by the model, the shape of the single sample of input data when making the prediction must be [1, 3] for the 1 sample and 3 time steps (features) of the input and the single feature.
# demonstrate prediction x_input = array([70, 80, 90]) x_input = x_input.reshape((1, n_steps_in)) yhat = model.predict(x_input, verbose=0)
Tying all of this together, the MLP for multi-step forecasting with a univariate time series is listed below.
# univariate multi-step vector-output mlp example from numpy import array from keras.models import Sequential from keras.layers import Dense # split a univariate sequence into samples def split_sequence(sequence, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out # check if we are beyond the sequence if out_end_ix > len(sequence): break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix:out_end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90] # choose a number of time steps n_steps_in, n_steps_out = 3, 2 # split into samples X, y = split_sequence(raw_seq, n_steps_in, n_steps_out) # define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_steps_in)) model.add(Dense(n_steps_out)) model.compile(optimizer='adam', loss='mse') # fit model model.fit(X, y, epochs=2000, verbose=0) # demonstrate prediction x_input = array([70, 80, 90]) x_input = x_input.reshape((1, n_steps_in)) yhat = model.predict(x_input, verbose=0) print(yhat)
Running the example forecasts and prints the next two time steps in the sequence.
[[102.572365 113.88405 ]]
Multivariate Multi-Step MLP Models
In the previous sections, we have looked at univariate, multivariate, and multi-step time series forecasting.
It is possible to mix and match the different types of MLP models presented so far for the different problems. This too applies to time series forecasting problems that involve multivariate and multi-step forecasting, but it may be a little more challenging, particularly in preparing the data and defining the shape of inputs and outputs for the model.
In this section, we will look at short examples of data preparation and modeling for multivariate multi-step time series forecasting as a template to ease this challenge, specifically:
- Multiple Input Multi-Step Output.
- Multiple Parallel Input and Multi-Step Output.
Perhaps the biggest stumbling block is in the preparation of data, so this is where we will focus our attention.
Multiple Input Multi-Step Output
There are those multivariate time series forecasting problems where the output series is separate but dependent upon the input time series, and multiple time steps are required for the output series.
For example, consider our multivariate time series from a prior section:
[[ 10 15 25] [ 20 25 45] [ 30 35 65] [ 40 45 85] [ 50 55 105] [ 60 65 125] [ 70 75 145] [ 80 85 165] [ 90 95 185]]
We may use three prior time steps of each of the two input time series to predict two time steps of the output time series.
Input:
10, 15 20, 25 30, 35
Output:
65 85
The split_sequences() function below implements this behavior.
# split a multivariate sequence into samples def split_sequences(sequences, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out-1 # check if we are beyond the dataset if out_end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1] X.append(seq_x) y.append(seq_y) return array(X), array(y)
We can demonstrate this on our contrived dataset. The complete example is listed below.
# multivariate multi-step data preparation from numpy import array from numpy import hstack # split a multivariate sequence into samples def split_sequences(sequences, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out-1 # check if we are beyond the dataset if out_end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps_in, n_steps_out = 3, 2 # convert into input/output X, y = split_sequences(dataset, n_steps_in, n_steps_out) print(X.shape, y.shape) # summarize the data for i in range(len(X)): print(X[i], y[i])
Running the example first prints the shape of the prepared training data.
We can see that the shape of the input portion of the samples is three-dimensional, comprised of six samples, with three time steps and two variables for the two input time series.
The output portion of the samples is two-dimensional for the six samples and the two time steps for each sample to be predicted.
The prepared samples are then printed to confirm that the data was prepared as we specified.
(6, 3, 2) (6, 2) [[10 15] [20 25] [30 35]] [65 85] [[20 25] [30 35] [40 45]] [ 85 105] [[30 35] [40 45] [50 55]] [105 125] [[40 45] [50 55] [60 65]] [125 145] [[50 55] [60 65] [70 75]] [145 165] [[60 65] [70 75] [80 85]] [165 185]
We can now develop an MLP model for multi-step predictions using a vector output.
The complete example is listed below.
# multivariate multi-step mlp example from numpy import array from numpy import hstack from keras.models import Sequential from keras.layers import Dense # split a multivariate sequence into samples def split_sequences(sequences, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out-1 # check if we are beyond the dataset if out_end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :-1], sequences[end_ix-1:out_end_ix, -1] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps_in, n_steps_out = 3, 2 # convert into input/output X, y = split_sequences(dataset, n_steps_in, n_steps_out) # flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input)) # define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_input)) model.add(Dense(n_steps_out)) model.compile(optimizer='adam', loss='mse') # fit model model.fit(X, y, epochs=2000, verbose=0) # demonstrate prediction x_input = array([[70, 75], [80, 85], [90, 95]]) x_input = x_input.reshape((1, n_input)) yhat = model.predict(x_input, verbose=0) print(yhat)
Running the example fits the model and predicts the next two time steps of the output sequence beyond the dataset.
We would expect the next two steps to be [185, 205].
It is a challenging framing of the problem with very little data, and the arbitrarily configured version of the model gets close.
[[186.53822 208.41725]]
Multiple Parallel Input and Multi-Step Output
A problem with parallel time series may require the prediction of multiple time steps of each time series.
For example, consider our multivariate time series from a prior section:
[[ 10 15 25] [ 20 25 45] [ 30 35 65] [ 40 45 85] [ 50 55 105] [ 60 65 125] [ 70 75 145] [ 80 85 165] [ 90 95 185]]
We may use the last three time steps from each of the three time series as input to the model and predict the next time steps of each of the three time series as output.
The first sample in the training dataset would be the following.
Input:
10, 15, 25 20, 25, 45 30, 35, 65
Output:
40, 45, 85 50, 55, 105
The split_sequences() function below implements this behavior.
# split a multivariate sequence into samples def split_sequences(sequences, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out # check if we are beyond the dataset if out_end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :] X.append(seq_x) y.append(seq_y) return array(X), array(y)
We can demonstrate this function on the small contrived dataset.
The complete example is listed below.
# multivariate multi-step data preparation from numpy import array from numpy import hstack # split a multivariate sequence into samples def split_sequences(sequences, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out # check if we are beyond the dataset if out_end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps_in, n_steps_out = 3, 2 # convert into input/output X, y = split_sequences(dataset, n_steps_in, n_steps_out) print(X.shape, y.shape) # summarize the data for i in range(len(X)): print(X[i], y[i])
Running the example first prints the shape of the prepared training dataset.
We can see that both the input (X) and output (Y) elements of the dataset are three dimensional for the number of samples, time steps, and variables or parallel time series respectively.
The input and output elements of each series are then printed side by side so that we can confirm that the data was prepared as we expected.
(5, 3, 3) (5, 2, 3) [[10 15 25] [20 25 45] [30 35 65]] [[ 40 45 85] [ 50 55 105]] [[20 25 45] [30 35 65] [40 45 85]] [[ 50 55 105] [ 60 65 125]] [[ 30 35 65] [ 40 45 85] [ 50 55 105]] [[ 60 65 125] [ 70 75 145]] [[ 40 45 85] [ 50 55 105] [ 60 65 125]] [[ 70 75 145] [ 80 85 165]] [[ 50 55 105] [ 60 65 125] [ 70 75 145]] [[ 80 85 165] [ 90 95 185]]
We can now develop an MLP model to make multivariate multi-step forecasts.
In addition to flattening the shape of the input data, as we have in prior examples, we must also flatten the three-dimensional structure of the output data. This is because the MLP model is only capable of taking vector inputs and outputs.
# flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input)) # flatten output n_output = y.shape[1] * y.shape[2] y = y.reshape((y.shape[0], n_output))
The complete example is listed below.
# multivariate multi-step mlp example from numpy import array from numpy import hstack from keras.models import Sequential from keras.layers import Dense # split a multivariate sequence into samples def split_sequences(sequences, n_steps_in, n_steps_out): X, y = list(), list() for i in range(len(sequences)): # find the end of this pattern end_ix = i + n_steps_in out_end_ix = end_ix + n_steps_out # check if we are beyond the dataset if out_end_ix > len(sequences): break # gather input and output parts of the pattern seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix:out_end_ix, :] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90]) in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95]) out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))]) # convert to [rows, columns] structure in_seq1 = in_seq1.reshape((len(in_seq1), 1)) in_seq2 = in_seq2.reshape((len(in_seq2), 1)) out_seq = out_seq.reshape((len(out_seq), 1)) # horizontally stack columns dataset = hstack((in_seq1, in_seq2, out_seq)) # choose a number of time steps n_steps_in, n_steps_out = 3, 2 # convert into input/output X, y = split_sequences(dataset, n_steps_in, n_steps_out) # flatten input n_input = X.shape[1] * X.shape[2] X = X.reshape((X.shape[0], n_input)) # flatten output n_output = y.shape[1] * y.shape[2] y = y.reshape((y.shape[0], n_output)) # define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_input)) model.add(Dense(n_output)) model.compile(optimizer='adam', loss='mse') # fit model model.fit(X, y, epochs=2000, verbose=0) # demonstrate prediction x_input = array([[60, 65, 125], [70, 75, 145], [80, 85, 165]]) x_input = x_input.reshape((1, n_input)) yhat = model.predict(x_input, verbose=0) print(yhat)
Running the example fits the model and predicts the values for each of the three time steps for the next two time steps beyond the end of the dataset.
We would expect the values for these series and time steps to be as follows:
90, 95, 185 100, 105, 205
We can see that the model forecast gets reasonably close to the expected values.
[[ 91.28376 96.567 188.37575 100.54482 107.9219 208.108 ]
Summary
In this tutorial, you discovered how to develop a suite of Multilayer Perceptron, or MLP, models for a range of standard time series forecasting problems.
Specifically, you learned:
- How to develop MLP models for univariate time series forecasting.
- How to develop MLP models for multivariate time series forecasting.
- How to develop MLP models for multi-step time series forecasting.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post How to Develop Multilayer Perceptron Models for Time Series Forecasting appeared first on Machine Learning Mastery.
