Author: Jason Brownlee
The Dogs vs. Cats dataset is a standard computer vision dataset that involves classifying photos as either containing a dog or cat.
Although the problem sounds simple, it was only effectively addressed in the last few years using deep learning convolutional neural networks. While the dataset is effectively solved, it can be used as the basis for learning and practicing how to develop, evaluate, and use convolutional deep learning neural networks for image classification from scratch.
This includes how to develop a robust test harness for estimating the performance of the model, how to explore improvements to the model, and how to save the model and later load it to make predictions on new data.
In this tutorial, you will discover how to develop a convolutional neural network to classify photos of dogs and cats.
After completing this tutorial, you will know:
- How to load and prepare photos of dogs and cats for modeling.
- How to develop a convolutional neural network for photo classification from scratch and improve model performance.
- How to develop a model for photo classification using transfer learning.
Let’s get started.

How to Develop a Convolutional Neural Network to Classify Photos of Dogs and Cats
Photo by Cohen Van der Velde, some rights reserved.
Tutorial Overview
This tutorial is divided into six parts; they are:
- Dogs vs. Cats Prediction Problem
- Dogs vs. Cats Dataset Preparation
- Develop a Baseline CNN Model
- Develop Model Improvements
- Explore Transfer Learning
- How to Finalize the Model and Make Predictions
Dogs vs. Cats Prediction Problem
The dogs vs cats dataset refers to a dataset used for a Kaggle machine learning competition held in 2013.
The dataset is comprised of photos of dogs and cats provided as a subset of photos from a much larger dataset of 3 million manually annotated photos. The dataset was developed as a partnership between Petfinder.com and Microsoft.
The dataset was originally used as a CAPTCHA (or Completely Automated Public Turing test to tell Computers and Humans Apart), that is, a task that it is believed a human finds trivial, but cannot be solved by a machine, used on websites to distinguish between human users and bots. Specifically, the task was referred to as “Asirra” or Animal Species Image Recognition for Restricting Access, a type of CAPTCHA. The task was described in the 2007 paper titled “Asirra: A CAPTCHA that Exploits Interest-Aligned Manual Image Categorization“.
We present Asirra, a CAPTCHA that asks users to identify cats out of a set of 12 photographs of both cats and dogs. Asirra is easy for users; user studies indicate it can be solved by humans 99.6% of the time in under 30 seconds. Barring a major advance in machine vision, we expect computers will have no better than a 1/54,000 chance of solving it.
— Asirra: A CAPTCHA that Exploits Interest-Aligned Manual Image Categorization, 2007.
At the time that the competition was posted, the state-of-the-art result was achieved with an SVM and described in a 2007 paper with the title “Machine Learning Attacks Against the Asirra CAPTCHA” (PDF) that achieved 80% classification accuracy. It was this paper that demonstrated that the task was no longer a suitable task for a CAPTCHA soon after the task was proposed.
… we describe a classifier which is 82.7% accurate in telling apart the images of cats and dogs used in Asirra. This classifier is a combination of support-vector machine classifiers trained on color and texture features extracted from images. […] Our results suggest caution against deploying Asirra without safeguards.
— Machine Learning Attacks Against the Asirra CAPTCHA, 2007.
The Kaggle competition provided 25,000 labeled photos: 12,500 dogs and the same number of cats. Predictions were then required on a test dataset of 12,500 unlabeled photographs. The competition was won by Pierre Sermanet (currently a research scientist at Google Brain) who achieved a classification accuracy of about 98.914% on a 70% subsample of the test dataset. His method was later described as part of the 2013 paper titled “OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks.”
The dataset is straightforward to understand and small enough to fit into memory. As such, it has become a good “hello world” or “getting started” computer vision dataset for beginners when getting started with convolutional neural networks.
As such, it is routine to achieve approximately 80% accuracy with a manually designed convolutional neural network and 90%+ accuracy using transfer learning on this task.
Want Results with Deep Learning for Computer Vision?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Dogs vs. Cats Dataset Preparation
The dataset can be downloaded for free from the Kaggle website, although I believe you must have a Kaggle account.
If you do not have a Kaggle account, sign-up first.
Download the dataset by visiting the Dogs vs. Cats Data page and click the “Download All” button.
This will download the 850-megabyte file “dogs-vs-cats.zip” to your workstation.
Unzip the file and you will see train.zip, train1.zip and a .csv file. Unzip the train.zip file, as we will be focusing only on this dataset.
You will now have a folder called ‘train/‘ that contains 25,000 .jpg files of dogs and cats. The photos are labeled by their filename, with the word “dog” or “cat“. The file naming convention is as follows:
cat.0.jpg ... cat.124999.jpg dog.0.jpg dog.124999.jpg
Plot Dog and Cat Photos
Looking at a few random photos in the directory, you can see that the photos are color and have different shapes and sizes.
For example, let’s load and plot the first nine photos of dogs in a single figure.
The complete example is listed below.
# plot dog photos from the dogs vs cats dataset from matplotlib import pyplot from matplotlib.image import imread # define location of dataset folder = 'train/' # plot first few images for i in range(9): # define subplot pyplot.subplot(330 + 1 + i) # define filename filename = folder + 'dog.' + str(i) + '.jpg' # load image pixels image = imread(filename) # plot raw pixel data pyplot.imshow(image) # show the figure pyplot.show()
Running the example creates a figure showing the first nine photos of dogs in the dataset.
We can see that some photos are landscape format, some are portrait format, and some are square.
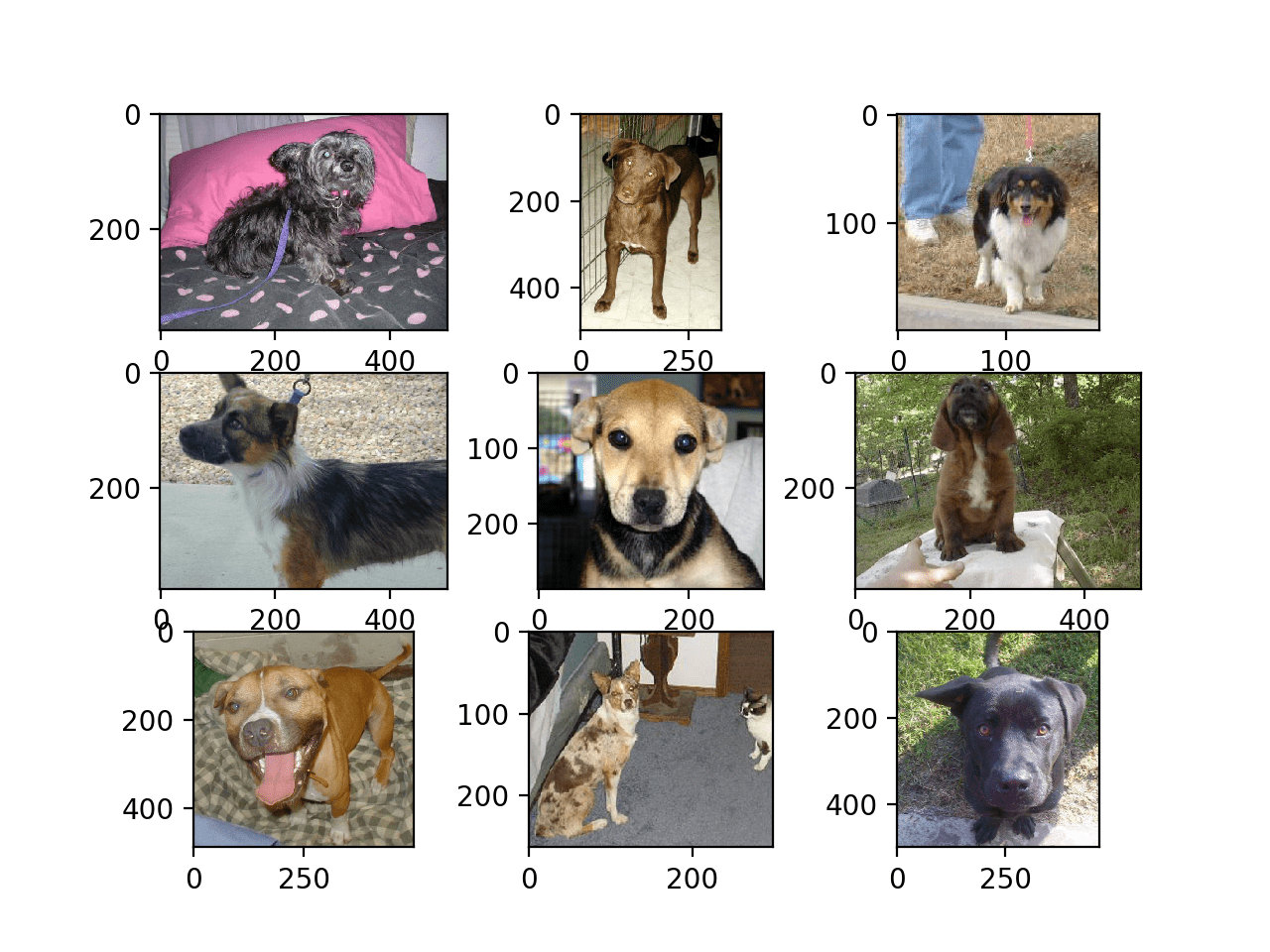
Plot of the First Nine Photos of Dogs in the Dogs vs Cats Dataset
We can update the example and change it to plot cat photos instead; the complete example is listed below.
# plot cat photos from the dogs vs cats dataset from matplotlib import pyplot from matplotlib.image import imread # define location of dataset folder = 'train/' # plot first few images for i in range(9): # define subplot pyplot.subplot(330 + 1 + i) # define filename filename = folder + 'cat.' + str(i) + '.jpg' # load image pixels image = imread(filename) # plot raw pixel data pyplot.imshow(image) # show the figure pyplot.show()
Again, we can see that the photos are all different sizes.
We can also see a photo where the cat is barely visible (bottom left corner) and another that has two cats (lower right corner). This suggests that any classifier fit on this problem will have to be robust.

Plot of the First Nine Photos of Cats in the Dogs vs Cats Dataset
Select Standardized Photo Size
The photos will have to be reshaped prior to modeling so that all images have the same shape. This is often a small square image.
There are many ways to achieve this, although the most common is a simple resize operation that will stretch and deform the aspect ratio of each image and force it into the new shape.
We could load all photos and look at the distribution of the photo widths and heights, then design a new photo size that best reflects what we are most likely to see in practice.
Smaller inputs mean a model that is faster to train, and typically this concern dominates the choice of image size. In this case, we will follow this approach and choose a fixed size of 200×200 pixels.
Pre-Process Photo Sizes (Optional)
If we want to load all of the images into memory, we can estimate that it would require about 12 gigabytes of RAM.
That is 25,000 images with 200x200x3 pixels each, or 3,000,000,000 32-bit pixel values.
We could load all of the images, reshape them, and store them as a single NumPy array. This could fit into RAM on many modern machines, but not all, especially if you only have 8 gigabytes to work with.
We can write custom code to load the images into memory and resize them as part of the loading process, then save them ready for modeling.
The example below uses the Keras image processing API to load all 25,000 photos in the training dataset and reshapes them to 200×200 square photos. The label is also determined for each photo based on the filenames. A tuple of photos and labels is then saved.
# load dogs vs cats dataset, reshape and save to a new file
from os import listdir
from numpy import asarray
from numpy import save
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
# define location of dataset
folder = 'train/'
photos, labels = list(), list()
# enumerate files in the directory
for file in listdir(folder):
# determine class
output = 0.0
if file.startswith('cat'):
output = 1.0
# load image
photo = load_img(folder + file, target_size=(200, 200))
# convert to numpy array
photo = img_to_array(photo)
# store
photos.append(photo)
labels.append(output)
# convert to a numpy arrays
photos = asarray(photos)
labels = asarray(labels)
print(photos.shape, labels.shape)
# save the reshaped photos
save('dogs_vs_cats_photos.npy', photos)
save('dogs_vs_cats_labels.npy', labels)
Running the example may take about one minute to load all of the images into memory and prints the shape of the loaded data to confirm it was loaded correctly.
Note: running this example assumes you have more than 12 gigabytes of RAM. You can skip this example if you do not have sufficient RAM; it is only provided as a demonstration.
(25000, 200, 200, 3) (25000,)
At the end of the run, two files with the names ‘dogs_vs_cats_photos.npy‘ and ‘dogs_vs_cats_labels.npy‘ are created that contain all of the resized images and their associated class labels. The files are only about 12 gigabytes in size together and are significantly faster to load than the individual images.
The prepared data can be loaded directly; for example:
# load and confirm the shape
from numpy import load
photos = load('dogs_vs_cats_photos.npy')
labels = load('dogs_vs_cats_labels.npy')
print(photos.shape, labels.shape)
Pre-Process Photos into Standard Directories
Alternately, we can load the images progressively using the Keras ImageDataGenerator class and flow_from_directory() API. This will be slower to execute but will run on more machines.
This API prefers data to be divided into separate train/ and test/ directories, and under each directory to have a subdirectory for each class, e.g. a train/dog/ and a train/cat/ subdirectories and the same for test. Images are then organized under the subdirectories.
We can write a script to create a copy of the dataset with this preferred structure. We will randomly select 25% of the images (or 6,250) to be used in a test dataset.
First, we need to create the directory structure as follows:
dataset_dogs_vs_cats
├── test
│ ├── cats
│ └── dogs
└── train
├── cats
└── dogs
We can create directories in Python using the makedirs() function and use a loop to create the dog/ and cat/ subdirectories for both the train/ and test/ directories.
# create directories dataset_home = 'dataset_dogs_vs_cats/' subdirs = ['train/', 'test/'] for subdir in subdirs: # create label subdirectories labeldirs = ['dogs/', 'cats/'] for labldir in labeldirs: newdir = dataset_home + subdir + labldir makedirs(newdir, exist_ok=True)
Next, we can enumerate all image files in the dataset and copy them into the dogs/ or cats/ subdirectory based on their filename.
Additionally, we can randomly decide to hold back 25% of the images into the test dataset. This is done consistently by fixing the seed for the pseudorandom number generator so that we get the same split of data each time the code is run.
# seed random number generator
seed(1)
# define ratio of pictures to use for validation
val_ratio = 0.25
# copy training dataset images into subdirectories
src_directory = 'train/'
for file in listdir(src_directory):
src = src_directory + '/' + file
dst_dir = 'train/'
if random() < val_ratio:
dst_dir = 'test/'
if file.startswith('cat'):
dst = dataset_home + dst_dir + 'cats/' + file
copyfile(src, dst)
elif file.startswith('dog'):
dst = dataset_home + dst_dir + 'dogs/' + file
copyfile(src, dst)
The complete code example is listed below and assumes that you have the images in the downloaded train.zip unzipped in the current working directory in train/.
# organize dataset into a useful structure
from os import makedirs
from os import listdir
from shutil import copyfile
from random import seed
from random import random
# create directories
dataset_home = 'dataset_dogs_vs_cats/'
subdirs = ['train/', 'test/']
for subdir in subdirs:
# create label subdirectories
labeldirs = ['dogs/', 'cats/']
for labldir in labeldirs:
newdir = dataset_home + subdir + labldir
makedirs(newdir, exist_ok=True)
# seed random number generator
seed(1)
# define ratio of pictures to use for validation
val_ratio = 0.25
# copy training dataset images into subdirectories
src_directory = 'train/'
for file in listdir(src_directory):
src = src_directory + '/' + file
dst_dir = 'train/'
if random() < val_ratio:
dst_dir = 'test/'
if file.startswith('cat'):
dst = dataset_home + dst_dir + 'cats/' + file
copyfile(src, dst)
elif file.startswith('dog'):
dst = dataset_home + dst_dir + 'dogs/' + file
copyfile(src, dst)
After running the example, you will now have a new dataset_dogs_vs_cats/ directory with a train/ and val/ subfolders and further dogs/ can cats/ subdirectories, exactly as designed.
Develop a Baseline CNN Model
In this section, we can develop a baseline convolutional neural network model for the dogs vs. cats dataset.
A baseline model will establish a minimum model performance to which all of our other models can be compared, as well as a model architecture that we can use as the basis of study and improvement.
A good starting point is the general architectural principles of the VGG models. These are a good starting point because they achieved top performance in the ILSVRC 2014 competition and because the modular structure of the architecture is easy to understand and implement. For more details on the VGG model, see the 2015 paper “Very Deep Convolutional Networks for Large-Scale Image Recognition.”
The architecture involves stacking convolutional layers with small 3×3 filters followed by a max pooling layer. Together, these layers form a block, and these blocks can be repeated where the number of filters in each block is increased with the depth of the network such as 32, 64, 128, 256 for the first four blocks of the model. Padding is used on the convolutional layers to ensure the height and width shapes of the output feature maps matches the inputs.
We can explore this architecture on the dogs vs cats problem and compare a model with this architecture with 1, 2, and 3 blocks.
Each layer will use the ReLU activation function and the He weight initialization, which are generally best practices. For example, a 3-block VGG-style architecture where each block has a single convolutional and pooling layer can be defined in Keras as follows:
# block 1 model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3))) model.add(MaxPooling2D((2, 2))) # block 2 model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) # block 3 model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2)))
We can create a function named define_model() that will define a model and return it ready to be fit on the dataset. This function can then be customized to define different baseline models, e.g. versions of the model with 1, 2, or 3 VGG style blocks.
The model will be fit with stochastic gradient descent and we will start with a conservative learning rate of 0.001 and a momentum of 0.9.
The problem is a binary classification task, requiring the prediction of one value of either 0 or 1. An output layer with 1 node and a sigmoid activation will be used and the model will be optimized using the binary cross-entropy loss function.
Below is an example of the define_model() function for defining a convolutional neural network model for the dogs vs. cats problem with one vgg-style block.
# define cnn model def define_model(): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3))) model.add(MaxPooling2D((2, 2))) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='sigmoid')) # compile model opt = SGD(lr=0.001, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy']) return model
It can be called to prepare a model as needed, for example:
# define model model = define_model()
Next, we need to prepare the data.
This involves first defining an instance of the ImageDataGenerator that will scale the pixel values to the range of 0-1.
# create data generator datagen = ImageDataGenerator(rescale=1.0/255.0)
Next, iterators need to be prepared for both the train and test datasets.
We can use the flow_from_directory() function on the data generator and create one iterator for each of the train/ and test/ directories. We must specify that the problem is a binary classification problem via the “class_mode” argument, and to load the images with the size of 200×200 pixels via the “target_size” argument. We will fix the batch size at 64.
# prepare iterators
train_it = datagen.flow_from_directory('dataset_dogs_vs_cats/train/',
class_mode='binary', batch_size=64, target_size=(200, 200))
test_it = datagen.flow_from_directory('dataset_dogs_vs_cats/test/',
class_mode='binary', batch_size=64, target_size=(200, 200))
We can then fit the model using the train iterator (train_it) and use the test iterator (test_it) as a validation dataset during training.
The number of steps for the train and test iterators must be specified. This is the number of batches that will comprise one epoch. This can be specified via the length of each iterator, and will be the total number of images in the train and test directories divided by the batch size (64).
The model will be fit for 20 epochs, a small number to check if the model can learn the problem.
# fit model history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=20, verbose=0)
Once fit, the final model can be evaluated on the test dataset directly and the classification accuracy reported.
# evaluate model
_, acc = model.evaluate_generator(test_it, steps=len(test_it), verbose=0)
print('> %.3f' % (acc * 100.0))
Finally, we can create a plot of the history collected during training stored in the “history” directory returned from the call to fit_generator().
The History contains the model accuracy and loss on the test and training dataset at the end of each epoch. Line plots of these measures over training epochs provide learning curves that we can use to get an idea of whether the model is overfitting, underfitting, or has a good fit.
The summarize_diagnostics() function below takes the history directory and creates a single figure with a line plot of the loss and another for the accuracy. The figure is then saved to file with a filename based on the name of the script. This is helpful if we wish to evaluate many variations of the model in different files and create line plots automatically for each.
# plot diagnostic learning curves
def summarize_diagnostics(history):
# plot loss
pyplot.subplot(211)
pyplot.title('Cross Entropy Loss')
pyplot.plot(history.history['loss'], color='blue', label='train')
pyplot.plot(history.history['val_loss'], color='orange', label='test')
# plot accuracy
pyplot.subplot(212)
pyplot.title('Classification Accuracy')
pyplot.plot(history.history['acc'], color='blue', label='train')
pyplot.plot(history.history['val_acc'], color='orange', label='test')
# save plot to file
filename = sys.argv[0].split('/')[-1]
pyplot.savefig(filename + '_plot.png')
pyplot.close()
We can tie all of this together into a simple test harness for testing a model configuration.
The complete example of evaluating a one-block baseline model on the dogs and cats dataset is listed below.
# baseline model for the dogs vs cats dataset
import sys
from matplotlib import pyplot
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Dense
from keras.layers import Flatten
from keras.optimizers import SGD
from keras.preprocessing.image import ImageDataGenerator
# define cnn model
def define_model():
model = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3)))
model.add(MaxPooling2D((2, 2)))
model.add(Flatten())
model.add(Dense(128, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='sigmoid'))
# compile model
opt = SGD(lr=0.001, momentum=0.9)
model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy'])
return model
# plot diagnostic learning curves
def summarize_diagnostics(history):
# plot loss
pyplot.subplot(211)
pyplot.title('Cross Entropy Loss')
pyplot.plot(history.history['loss'], color='blue', label='train')
pyplot.plot(history.history['val_loss'], color='orange', label='test')
# plot accuracy
pyplot.subplot(212)
pyplot.title('Classification Accuracy')
pyplot.plot(history.history['acc'], color='blue', label='train')
pyplot.plot(history.history['val_acc'], color='orange', label='test')
# save plot to file
filename = sys.argv[0].split('/')[-1]
pyplot.savefig(filename + '_plot.png')
pyplot.close()
# run the test harness for evaluating a model
def run_test_harness():
# define model
model = define_model()
# create data generator
datagen = ImageDataGenerator(rescale=1.0/255.0)
# prepare iterators
train_it = datagen.flow_from_directory('dataset_dogs_vs_cats/train/',
class_mode='binary', batch_size=64, target_size=(200, 200))
test_it = datagen.flow_from_directory('dataset_dogs_vs_cats/test/',
class_mode='binary', batch_size=64, target_size=(200, 200))
# fit model
history = model.fit_generator(train_it, steps_per_epoch=len(train_it),
validation_data=test_it, validation_steps=len(test_it), epochs=20, verbose=0)
# evaluate model
_, acc = model.evaluate_generator(test_it, steps=len(test_it), verbose=0)
print('> %.3f' % (acc * 100.0))
# learning curves
summarize_diagnostics(history)
# entry point, run the test harness
run_test_harness()
Now that we have a test harness, let’s look at the evaluation of three simple baseline models.
One Block VGG Model
The one-block VGG model has a single convolutional layer with 32 filters followed by a max pooling layer.
The define_model() function for this model was defined in the previous section but is provided again below for completeness.
# define cnn model def define_model(): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3))) model.add(MaxPooling2D((2, 2))) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='sigmoid')) # compile model opt = SGD(lr=0.001, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy']) return model
Running this example first prints the size of the train and test datasets, confirming that the dataset was loaded correctly.
The model is then fit and evaluated, which takes approximately 20 minutes on modern GPU hardware.
Found 18697 images belonging to 2 classes. Found 6303 images belonging to 2 classes. > 72.331
Your specific results may differ given the stochastic nature of the learning algorithm.
In this case, we can see that the model achieved an accuracy of about 72% on the test dataset.
A figure is also created showing a line plot for the loss and another for the accuracy of the model on both the train (blue) and test (orange) datasets.
Reviewing this plot, we can see that the model has overfit the training dataset at about 12 epochs.
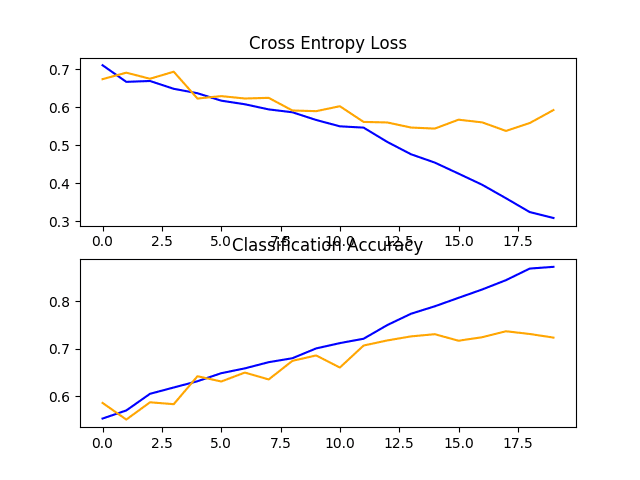
Line Plots of Loss and Accuracy Learning Curves for the Baseline Model With One VGG Block on the Dogs and Cats Dataset
Two Block VGG Model
The two-block VGG model extends the one block model and adds a second block with 64 filters.
The define_model() function for this model is provided below for completeness.
# define cnn model def define_model(): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3))) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='sigmoid')) # compile model opt = SGD(lr=0.001, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy']) return model
Running this example again prints the size of the train and test datasets, confirming that the dataset was loaded correctly.
The model is fit and evaluated and the performance on the test dataset is reported.
Found 18697 images belonging to 2 classes. Found 6303 images belonging to 2 classes. > 76.646
Your specific results may differ given the stochastic nature of the learning algorithm.
In this case, we can see that the model achieved a small improvement in performance from about 72% with one block to about 76% accuracy with two blocks
Reviewing the plot of the learning curves, we can see that again the model appears to have overfit the training dataset, perhaps sooner, in this case at around eight training epochs.
This is likely the result of the increased capacity of the model, and we might expect this trend of sooner overfitting to continue with the next model.
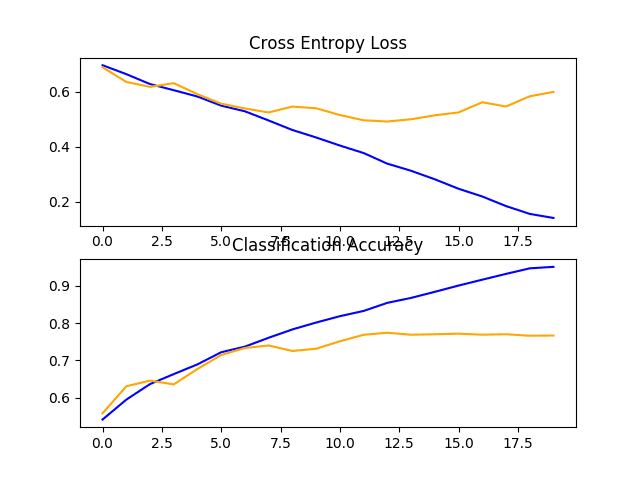
Line Plots of Loss and Accuracy Learning Curves for the Baseline Model With Two VGG Block on the Dogs and Cats Dataset
Three Block VGG Model
The three-block VGG model extends the two block model and adds a third block with 128 filters.
The define_model() function for this model was defined in the previous section but is provided again below for completeness.
# define cnn model def define_model(): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3))) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='sigmoid')) # compile model opt = SGD(lr=0.001, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy']) return model
Running this example prints the size of the train and test datasets, confirming that the dataset was loaded correctly.
The model is fit and evaluated and the performance on the test dataset is reported.
Found 18697 images belonging to 2 classes. Found 6303 images belonging to 2 classes. > 80.184
Your specific results may differ given the stochastic nature of the learning algorithm.
In this case, we can see that we achieved a further lift in performance from about 76% with two blocks to about 80% accuracy with three blocks. This result is good, as it is close to the prior state-of-the-art reported in the paper using an SVM at about 82% accuracy.
Reviewing the plot of the learning curves, we can see a similar trend of overfitting, in this case perhaps pushed back as far as to epoch five or six.
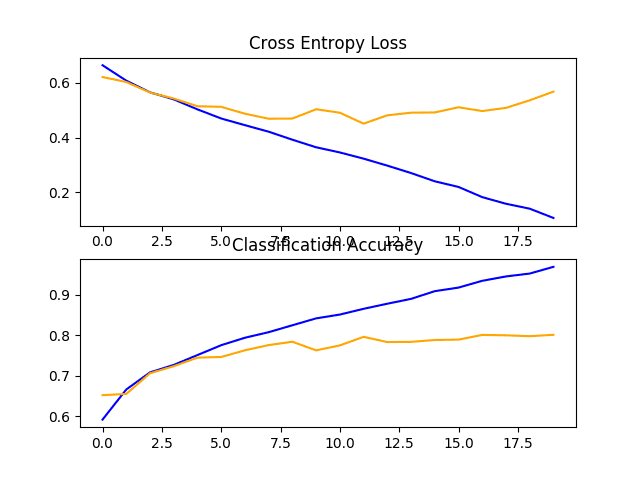
Line Plots of Loss and Accuracy Learning Curves for the Baseline Model With Three VGG Block on the Dogs and Cats Dataset
Discussion
We have explored three different models with a VGG-based architecture.
The results can be summarized below, although we must assume some variance in these results given the stochastic nature of the algorithm:
- VGG 1: 72.331%
- VGG 2: 76.646%
- VGG 3: 80.184%
We see a trend of improved performance with the increase in capacity, but also a similar case of overfitting occurring earlier and earlier in the run.
The results suggest that the model will likely benefit from regularization techniques. This may include techniques such as dropout, weight decay, and data augmentation. The latter can also boost performance by encouraging the model to learn features that are further invariant to position by expanding the training dataset.
Develop Model Improvements
In the previous section, we developed a baseline model using VGG-style blocks and discovered a trend of improved performance with increased model capacity.
In this section, we will start with the baseline model with three VGG blocks (i.e. VGG 3) and explore some simple improvements to the model.
From reviewing the learning curves for the model during training, the model showed strong signs of overfitting. We can explore two approaches to attempt to address this overfitting: dropout regularization and data augmentation.
Both of these approaches are expected to slow the rate of improvement during training and hopefully counter the overfitting of the training dataset. As such, we will increase the number of training epochs from 20 to 50 to give the model more space for refinement.
Dropout Regularization
Dropout regularization is a computationally cheap way to regularize a deep neural network.
Dropout works by probabilistically removing, or “dropping out,” inputs to a layer, which may be input variables in the data sample or activations from a previous layer. It has the effect of simulating a large number of networks with very different network structures and, in turn, making nodes in the network generally more robust to the inputs.
For more information on dropout, see the post:
Typically, a small amount of dropout can be applied after each VGG block, with more dropout applied to the fully connected layers near the output layer of the model.
Below is the define_model() function for an updated version of the baseline model with the addition of Dropout. In this case, a dropout of 20% is applied after each VGG block, with a larger dropout rate of 50% applied after the fully connected layer in the classifier part of the model.
# define cnn model def define_model(): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3))) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dropout(0.5)) model.add(Dense(1, activation='sigmoid')) # compile model opt = SGD(lr=0.001, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy']) return model
The full code listing of the baseline model with the addition of dropout on the dogs vs. cats dataset is listed below for completeness.
# baseline model with dropout for the dogs vs cats dataset
import sys
from matplotlib import pyplot
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import Dropout
from keras.optimizers import SGD
from keras.preprocessing.image import ImageDataGenerator
# define cnn model
def define_model():
model = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3)))
model.add(MaxPooling2D((2, 2)))
model.add(Dropout(0.2))
model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
model.add(MaxPooling2D((2, 2)))
model.add(Dropout(0.2))
model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
model.add(MaxPooling2D((2, 2)))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(128, activation='relu', kernel_initializer='he_uniform'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
# compile model
opt = SGD(lr=0.001, momentum=0.9)
model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy'])
return model
# plot diagnostic learning curves
def summarize_diagnostics(history):
# plot loss
pyplot.subplot(211)
pyplot.title('Cross Entropy Loss')
pyplot.plot(history.history['loss'], color='blue', label='train')
pyplot.plot(history.history['val_loss'], color='orange', label='test')
# plot accuracy
pyplot.subplot(212)
pyplot.title('Classification Accuracy')
pyplot.plot(history.history['acc'], color='blue', label='train')
pyplot.plot(history.history['val_acc'], color='orange', label='test')
# save plot to file
filename = sys.argv[0].split('/')[-1]
pyplot.savefig(filename + '_plot.png')
pyplot.close()
# run the test harness for evaluating a model
def run_test_harness():
# define model
model = define_model()
# create data generator
datagen = ImageDataGenerator(rescale=1.0/255.0)
# prepare iterator
train_it = datagen.flow_from_directory('dataset_dogs_vs_cats/train/',
class_mode='binary', batch_size=64, target_size=(200, 200))
test_it = datagen.flow_from_directory('dataset_dogs_vs_cats/test/',
class_mode='binary', batch_size=64, target_size=(200, 200))
# fit model
history = model.fit_generator(train_it, steps_per_epoch=len(train_it),
validation_data=test_it, validation_steps=len(test_it), epochs=50, verbose=0)
# evaluate model
_, acc = model.evaluate_generator(test_it, steps=len(test_it), verbose=0)
print('> %.3f' % (acc * 100.0))
# learning curves
summarize_diagnostics(history)
# entry point, run the test harness
run_test_harness()
Running the example first fits the model, then reports the model performance on the hold out test dataset.
Your specific results may vary given the stochastic nature of the learning algorithm.
In this case, we can see a small lift in model performance from about 80% accuracy for the baseline model to about 81% with the addition of dropout.
Found 18697 images belonging to 2 classes. Found 6303 images belonging to 2 classes. > 81.279
Reviewing the learning curves, we can see that dropout has had an effect on the rate of improvement of the model on both the train and test sets.
Overfitting has been reduced or delayed, although performance may begin to stall towards the end of the run.
The results suggest that further training epochs may result in further improvement of the model. It may also be interesting to explore perhaps a slightly higher dropout rate after the VGG blocks in addition to the increase in training epochs.
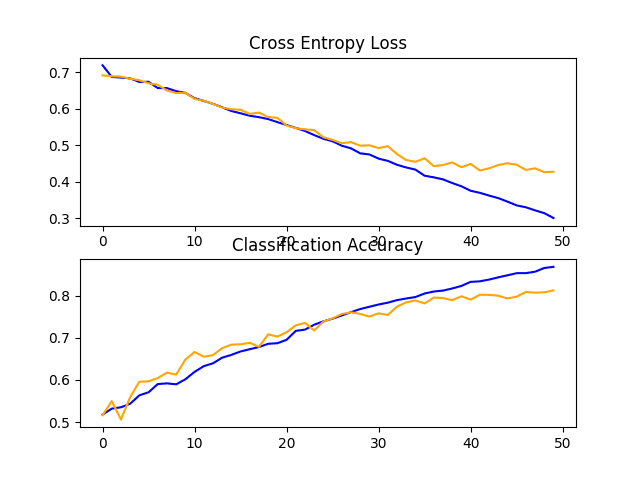
Line Plots of Loss and Accuracy Learning Curves for the Baseline Model With Dropout on the Dogs and Cats Dataset
Image Data Augmentation
Image data augmentation is a technique that can be used to artificially expand the size of a training dataset by creating modified versions of images in the dataset.
Training deep learning neural network models on more data can result in more skillful models, and the augmentation techniques can create variations of the images that can improve the ability of the fit models to generalize what they have learned to new images.
Data augmentation can also act as a regularization technique, adding noise to the training data, and encouraging the model to learn the same features, invariant to their position in the input.
Small changes to the input photos of dogs and cats might be useful for this problem, such as small shifts and horizontal flips. These augmentations can be specified as arguments to the ImageDataGenerator used for the training dataset. The augmentations should not be used for the test dataset, as we wish to evaluate the performance of the model on the unmodified photographs.
This requires that we have a separate ImageDataGenerator instance for the train and test dataset, then iterators for the train and test sets created from the respective data generators. For example:
# create data generators
train_datagen = ImageDataGenerator(rescale=1.0/255.0,
width_shift_range=0.1, height_shift_range=0.1, horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1.0/255.0)
# prepare iterators
train_it = train_datagen.flow_from_directory('dataset_dogs_vs_cats/train/',
class_mode='binary', batch_size=64, target_size=(200, 200))
test_it = test_datagen.flow_from_directory('dataset_dogs_vs_cats/test/',
class_mode='binary', batch_size=64, target_size=(200, 200))
In this case, photos in the training dataset will be augmented with small (10%) random horizontal and vertical shifts and random horizontal flips that create a mirror image of a photo. Photos in both the train and test steps will have their pixel values scaled in the same way.
The full code listing of the baseline model with training data augmentation for the dogs and cats dataset is listed below for completeness.
# baseline model with data augmentation for the dogs vs cats dataset
import sys
from matplotlib import pyplot
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Dense
from keras.layers import Flatten
from keras.optimizers import SGD
from keras.preprocessing.image import ImageDataGenerator
# define cnn model
def define_model():
model = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(200, 200, 3)))
model.add(MaxPooling2D((2, 2)))
model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
model.add(MaxPooling2D((2, 2)))
model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same'))
model.add(MaxPooling2D((2, 2)))
model.add(Flatten())
model.add(Dense(128, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='sigmoid'))
# compile model
opt = SGD(lr=0.001, momentum=0.9)
model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy'])
return model
# plot diagnostic learning curves
def summarize_diagnostics(history):
# plot loss
pyplot.subplot(211)
pyplot.title('Cross Entropy Loss')
pyplot.plot(history.history['loss'], color='blue', label='train')
pyplot.plot(history.history['val_loss'], color='orange', label='test')
# plot accuracy
pyplot.subplot(212)
pyplot.title('Classification Accuracy')
pyplot.plot(history.history['acc'], color='blue', label='train')
pyplot.plot(history.history['val_acc'], color='orange', label='test')
# save plot to file
filename = sys.argv[0].split('/')[-1]
pyplot.savefig(filename + '_plot.png')
pyplot.close()
# run the test harness for evaluating a model
def run_test_harness():
# define model
model = define_model()
# create data generators
train_datagen = ImageDataGenerator(rescale=1.0/255.0,
width_shift_range=0.1, height_shift_range=0.1, horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1.0/255.0)
# prepare iterators
train_it = train_datagen.flow_from_directory('dataset_dogs_vs_cats/train/',
class_mode='binary', batch_size=64, target_size=(200, 200))
test_it = test_datagen.flow_from_directory('dataset_dogs_vs_cats/test/',
class_mode='binary', batch_size=64, target_size=(200, 200))
# fit model
history = model.fit_generator(train_it, steps_per_epoch=len(train_it),
validation_data=test_it, validation_steps=len(test_it), epochs=50, verbose=0)
# evaluate model
_, acc = model.evaluate_generator(test_it, steps=len(test_it), verbose=0)
print('> %.3f' % (acc * 100.0))
# learning curves
summarize_diagnostics(history)
# entry point, run the test harness
run_test_harness()
Running the example first fits the model, then reports the model performance on the hold out test dataset.
Your specific results may vary given the stochastic nature of the learning algorithm.
In this case, we can see a lift in performance of about 5% from about 80% for the baseline model to about 85% for the baseline model with simple data augmentation.
> 85.816
Reviewing the learning curves, we can see that it appears the model is capable of further learning with both the loss on the train and test dataset still decreasing even at the end of the run. Repeating the experiment with 100 or more epochs will very likely result in a better performing model.
It may be interesting to explore other augmentations that may further encourage the learning of features invariant to their position in the input, such as minor rotations and zooms.
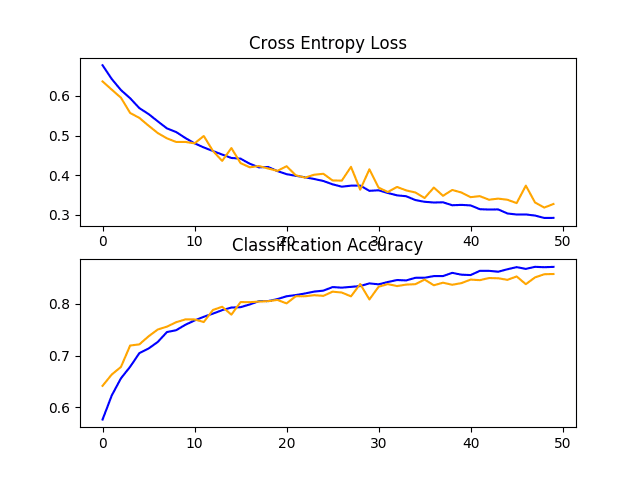
Line Plots of Loss and Accuracy Learning Curves for the Baseline Model With Data Augmentation on the Dogs and Cats Dataset
Discussion
We have explored three different improvements to the baseline model.
The results can be summarized below, although we must assume some variance in these results given the stochastic nature of the algorithm:
- Baseline VGG3 + Dropout: 81.279%
- Baseline VGG3 + Data Augmentation: 85.816
As suspected, the addition of regularization techniques slows the progression of the learning algorithms and reduces overfitting, resulting in improved performance on the holdout dataset. It is likely that the combination of both approaches with further increase in the number of training epochs will result in further improvements.
This is just the beginning of the types of improvements that can be explored on this dataset. In addition to tweaks to the regularization methods described, other regularization methods could be explored such as weight decay and early stopping.
It may be worth exploring changes to the learning algorithm such as changes to the learning rate, use of a learning rate schedule, or an adaptive learning rate such as Adam.
Alternate model architectures may also be worth exploring. The chosen baseline model is expected to offer more capacity than may be required for this problem and a smaller model may faster to train and in turn could result in better performance.
Explore Transfer Learning
Transfer learning involves using all or parts of a model trained on a related task.
Keras provides a range of pre-trained models that can be loaded and used wholly or partially via the Keras Applications API.
A useful model for transfer learning is one of the VGG models, such as VGG-16 with 16 layers that at the time it was developed, achieved top results on the ImageNet photo classification challenge.
The model is comprised of two main parts, the feature extractor part of the model that is made up of VGG blocks, and the classifier part of the model that is made up of fully connected layers and the output layer.
We can use the feature extraction part of the model and add a new classifier part of the model that is tailored to the dogs and cats dataset. Specifically, we can hold the weights of all of the convolutional layers fixed during training, and only train new fully connected layers that will learn to interpret the features extracted from the model and make a binary classification.
This can be achieved by loading the VGG-16 model, removing the fully connected layers from the output-end of the model, then adding the new fully connected layers to interpret the model output and make a prediction. The classifier part of the model can be removed automatically by setting the “include_top” argument to “False“, which also requires that the shape of the input also be specified for the model, in this case (224, 224, 3). This means that the loaded model ends at the last max pooling layer, after which we can manually add a Flatten layer and the new clasifier layers.
The define_model() function below implements this and returns a new model ready for training.
# define cnn model def define_model(): # load model model = VGG16(include_top=False, input_shape=(224, 224, 3)) # mark loaded layers as not trainable for layer in model.layers: layer.trainable = False # add new classifier layers flat1 = Flatten()(model.layers[-1].output) class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1) output = Dense(1, activation='sigmoid')(class1) # define new model model = Model(inputs=model.inputs, outputs=output) # compile model opt = SGD(lr=0.001, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy']) return model
Once created, we can train the model as before on the training dataset.
Not a lot of training will be required in this case, as only the new fully connected and output layer have trainable weights. As such, we will fix the number of training epochs at 10.
The VGG16 model was trained on a specific ImageNet challenge dataset. As such, it is configured to expected input images to have the shape 224×224 pixels. We will use this as the target size when loading photos from the dogs and cats dataset.
The model also expects images to be centered. That is, to have the mean pixel values from each channel (red, green, and blue) as calculated on the ImageNet training dataset subtracted from the input. Keras provides a function to perform this preparation for individual photos via the preprocess_input() function. Nevertheless, we can achieve the same effect with the ImageDataGenerator by setting the “featurewise_center” argument to “True” and manually specifying the mean pixel values to use when centering as the mean values from the ImageNet training dataset: [123.68, 116.779, 103.939].
The full code listing of the VGG model for transfer learning on the dogs vs. cats dataset is listed below.
# vgg16 model used for transfer learning on the dogs and cats dataset
import sys
from matplotlib import pyplot
from keras.utils import to_categorical
from keras.applications.vgg16 import VGG16
from keras.models import Model
from keras.layers import Dense
from keras.layers import Flatten
from keras.optimizers import SGD
from keras.preprocessing.image import ImageDataGenerator
# define cnn model
def define_model():
# load model
model = VGG16(include_top=False, input_shape=(224, 224, 3))
# mark loaded layers as not trainable
for layer in model.layers:
layer.trainable = False
# add new classifier layers
flat1 = Flatten()(model.layers[-1].output)
class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1)
output = Dense(1, activation='sigmoid')(class1)
# define new model
model = Model(inputs=model.inputs, outputs=output)
# compile model
opt = SGD(lr=0.001, momentum=0.9)
model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy'])
return model
# plot diagnostic learning curves
def summarize_diagnostics(history):
# plot loss
pyplot.subplot(211)
pyplot.title('Cross Entropy Loss')
pyplot.plot(history.history['loss'], color='blue', label='train')
pyplot.plot(history.history['val_loss'], color='orange', label='test')
# plot accuracy
pyplot.subplot(212)
pyplot.title('Classification Accuracy')
pyplot.plot(history.history['acc'], color='blue', label='train')
pyplot.plot(history.history['val_acc'], color='orange', label='test')
# save plot to file
filename = sys.argv[0].split('/')[-1]
pyplot.savefig(filename + '_plot.png')
pyplot.close()
# run the test harness for evaluating a model
def run_test_harness():
# define model
model = define_model()
# create data generator
datagen = ImageDataGenerator(featurewise_center=True)
# specify imagenet mean values for centering
datagen.mean = [123.68, 116.779, 103.939]
# prepare iterator
train_it = datagen.flow_from_directory('dataset_dogs_vs_cats/train/',
class_mode='binary', batch_size=64, target_size=(224, 224))
test_it = datagen.flow_from_directory('dataset_dogs_vs_cats/test/',
class_mode='binary', batch_size=64, target_size=(224, 224))
# fit model
history = model.fit_generator(train_it, steps_per_epoch=len(train_it),
validation_data=test_it, validation_steps=len(test_it), epochs=10, verbose=1)
# evaluate model
_, acc = model.evaluate_generator(test_it, steps=len(test_it), verbose=0)
print('> %.3f' % (acc * 100.0))
# learning curves
summarize_diagnostics(history)
# entry point, run the test harness
run_test_harness()
Running the example first fits the model, then reports the model performance on the hold out test dataset.
Your specific results may vary given the stochastic nature of the learning algorithm.
In this case, we can see that the model achieved very impressive results with a classification accuracy of about 97% on the holdout test dataset.
Found 18697 images belonging to 2 classes. Found 6303 images belonging to 2 classes. > 97.636
Reviewing the learning curves, we can see that the model fits the dataset quickly. It does not show strong overfitting, although the results suggest that perhaps additional capacity in the classifier and/or the use of regularization might be helpful.
There are many improvements that could be made to this approach, including adding dropout regularization to the classifier part of the model and perhaps even fine-tuning the weights of some or all of the layers in the feature detector part of the model.
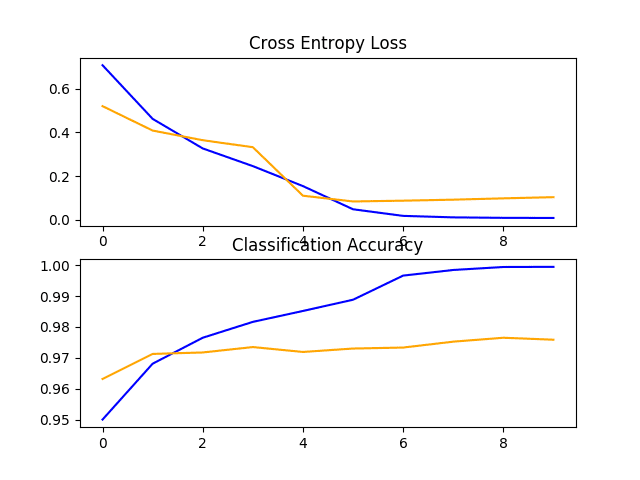
Line Plots of Loss and Accuracy Learning Curves for the VGG16 Transfer Learning Model on the Dogs and Cats Dataset
How to Finalize the Model and Make Predictions
The process of model improvement may continue for as long as we have ideas and the time and resources to test them out.
At some point, a final model configuration must be chosen and adopted. In this case, we will keep things simple and use the VGG-16 transfer learning approach as the final model.
First, we will finalize our model by fitting a model on the entire training dataset and saving the model to file for later use. We will then load the saved model and use it to make a prediction on a single image.
Prepare Final Dataset
A final model is typically fit on all available data, such as the combination of all train and test datasets.
In this tutorial, we will demonstrate the final model fit only on the training dataset as we only have labels for the training dataset.
The first step is to prepare the training dataset so that it can be loaded by the ImageDataGenerator class via flow_from_directory() function. Specifically, we need to create a new directory with all training images organized into dogs/ and cats/ subdirectories without any separation into train/ or test/ directories.
This can be achieved by updating the script we developed at the beginning of the tutorial. In this case, we will create a new finalize_dogs_vs_cats/ folder with dogs/ and cats/ subfolders for the entire training dataset.
The structure will look as follows:
finalize_dogs_vs_cats ├── cats └── dogs
The updated script is listed below for completeness.
# organize dataset into a useful structure
from os import makedirs
from os import listdir
from shutil import copyfile
# create directories
dataset_home = 'finalize_dogs_vs_cats/'
# create label subdirectories
labeldirs = ['dogs/', 'cats/']
for labldir in labeldirs:
newdir = dataset_home + labldir
makedirs(newdir, exist_ok=True)
# copy training dataset images into subdirectories
src_directory = 'dogs-vs-cats/train/'
for file in listdir(src_directory):
src = src_directory + '/' + file
if file.startswith('cat'):
dst = dataset_home + 'cats/' + file
copyfile(src, dst)
elif file.startswith('dog'):
dst = dataset_home + 'dogs/' + file
copyfile(src, dst)
Save Final Model
We are now ready to fit a final model on the entire training dataset.
The flow_from_directory() must be updated to load all of the images from the new finalize_dogs_vs_cats/ directory.
# prepare iterator
train_it = datagen.flow_from_directory('finalize_dogs_vs_cats/',
class_mode='binary', batch_size=64, target_size=(224, 224))
Additionally, the call to fit_generator() no longer needs to specify a validation dataset.
# fit model model.fit_generator(train_it, steps_per_epoch=len(train_it), epochs=10, verbose=0)
Once fit, we can save the final model to an H5 file by calling the save() function on the model and pass in the chosen filename.
# save model
model.save('final_model.h5')
Note, saving and loading a Keras model requires that the h5py library is installed on your workstation.
The complete example of fitting the final model on the training dataset and saving it to file is listed below.
# save the final model to file
from keras.applications.vgg16 import VGG16
from keras.models import Model
from keras.layers import Dense
from keras.layers import Flatten
from keras.optimizers import SGD
from keras.preprocessing.image import ImageDataGenerator
# define cnn model
def define_model():
# load model
model = VGG16(include_top=False, input_shape=(224, 224, 3))
# mark loaded layers as not trainable
for layer in model.layers:
layer.trainable = False
# add new classifier layers
flat1 = Flatten()(model.layers[-1].output)
class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1)
output = Dense(1, activation='sigmoid')(class1)
# define new model
model = Model(inputs=model.inputs, outputs=output)
# compile model
opt = SGD(lr=0.001, momentum=0.9)
model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy'])
return model
# run the test harness for evaluating a model
def run_test_harness():
# define model
model = define_model()
# create data generator
datagen = ImageDataGenerator(featurewise_center=True)
# specify imagenet mean values for centering
datagen.mean = [123.68, 116.779, 103.939]
# prepare iterator
train_it = datagen.flow_from_directory('finalize_dogs_vs_cats/',
class_mode='binary', batch_size=64, target_size=(224, 224))
# fit model
model.fit_generator(train_it, steps_per_epoch=len(train_it), epochs=10, verbose=0)
# save model
model.save('final_model.h5')
# entry point, run the test harness
run_test_harness()
After running this example, you will now have a large 81-megabyte file with the name ‘final_model.h5‘ in your current working directory.
Make Prediction
We can use our saved model to make a prediction on new images.
The model assumes that new images are color and they have been segmented so that one image contains at least one dog or cat.
Below is an image extracted from the test dataset for the dogs and cats competition. It has no label, but we can clearly tell it is a photo of a dog. You can save it in your current working directory with the filename ‘sample_image.jpg‘.

Dog (sample_image.jpg)
We will pretend this is an entirely new and unseen image, prepared in the required way, and see how we might use our saved model to predict the integer that the image represents. For this example, we expect class “1” for “Dog“.
Note: the subdirectories of images, one for each class, are loaded by the flow_from_directory() function in alphabetical order and assigned an integer for each class. The subdirectory “cat” comes before “dog“, therefore the class labels are assigned the integers: cat=0, dog=1. This can be changed via the “classes” argument in calling flow_from_directory() when training the model.
First, we can load the image and force it to the size to be 224×224 pixels. The loaded image can then be resized to have a single sample in a dataset. The pixel values must also be centered to match the way that the data was prepared during the training of the model. The load_image() function implements this and will return the loaded image ready for classification.
# load and prepare the image
def load_image(filename):
# load the image
img = load_img(filename, target_size=(224, 224))
# convert to array
img = img_to_array(img)
# reshape into a single sample with 3 channels
img = img.reshape(1, 224, 224, 3)
# center pixel data
img = img.astype('float32')
img = img - [123.68, 116.779, 103.939]
return img
Next, we can load the model as in the previous section and call the predict() function to predict the content in the image as a number between “0” and “1” for “cat” and “dog” respectively.
# predict the class result = model.predict(img)
The complete example is listed below.
# make a prediction for a new image.
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
from keras.models import load_model
# load and prepare the image
def load_image(filename):
# load the image
img = load_img(filename, target_size=(224, 224))
# convert to array
img = img_to_array(img)
# reshape into a single sample with 3 channels
img = img.reshape(1, 224, 224, 3)
# center pixel data
img = img.astype('float32')
img = img - [123.68, 116.779, 103.939]
return img
# load an image and predict the class
def run_example():
# load the image
img = load_image('sample_image.jpg')
# load model
model = load_model('final_model.h5')
# predict the class
result = model.predict(img)
print(result[0])
# entry point, run the example
run_example()
Running the example first loads and prepares the image, loads the model, and then correctly predicts that the loaded image represents a ‘dog‘ or class ‘1‘.
1
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Tune Regularization. Explore minor changes to the regularization techniques used on the baseline model, such as different dropout rates and different image augmentation.
- Tune Learning Rate. Explore changes to the learning algorithm used to train the baseline model, such as alternate learning rate, a learning rate schedule, or an adaptive learning rate algorithm such as Adam.
- Alternate Pre-Trained Model. Explore an alternate pre-trained model for transfer learning on the problem, such as Inception or ResNet.
If you explore any of these extensions, I’d love to know.
Post your findings in the comments below.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
- Asirra: A CAPTCHA that Exploits Interest-Aligned Manual Image Categorization, 2007.
- Machine Learning Attacks Against the Asirra CAPTCHA, 2007.
- OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks, 2013.
API
Articles
- Dogs vs Cats Kaggle Competition.
- Dogs vs. Cats Redux: Kernels Edition.
- Dogs vs Cats Dataset, Kaggle.
- Building powerful image classification models using very little data, 2016.
Summary
In this tutorial, you discovered how to develop a convolutional neural network to classify photos of dogs and cats.
Specifically, you learned:
- How to load and prepare photos of dogs and cats for modeling.
- How to develop a convolutional neural network for photo classification from scratch and improve model performance.
- How to develop a model for photo classification using transfer learning.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post How to Develop a Convolutional Neural Network to Classify Photos of Dogs and Cats (with 97% accuracy) appeared first on Machine Learning Mastery.
