Author: Jason Brownlee
Hill climbing the test set is an approach to achieving good or perfect predictions on a machine learning competition without touching the training set or even developing a predictive model.
As an approach to machine learning competitions, it is rightfully frowned upon, and most competition platforms impose limitations to prevent it, which is important.
Nevertheless, hill climbing the test set is something that a machine learning practitioner accidentally does as part of participating in a competition. By developing an explicit implementation to hill climb a test set, it helps to better understand how easy it can be to overfit a test dataset by overusing it to evaluate modeling pipelines.
In this tutorial, you will discover how to hill climb the test set for machine learning.
After completing this tutorial, you will know:
- Perfect predictions can be made by hill climbing the test set without even looking at the training dataset.
- How to hill climb the test set for classification and regression tasks.
- We implicitly hill climb the test set when we overuse the test set to evaluate our modeling pipelines.
Kick-start your project with my new book Data Preparation for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
How to Hill Climb the Test Set for Machine Learning
Photo by Stig Nygaard, some rights reserved.
Tutorial Overview
This tutorial is divided into five parts; they are:
- Hill Climb the Test Set
- Hill Climbing Algorithm
- How to Implement Hill Climbing
- Hill Climb Diabetes Classification Dataset
- Hill Climb Housing Regression Dataset
Hill Climb the Test Set
Machine learning competitions, like those on Kaggle, provide a complete training dataset as well as just the input for the test set.
The objective for a given competition is to predict target values, such as labels or numerical values for the test set. Solutions are evaluated against the hidden test set target values and scored appropriately. The submission with the best score against the test set wins the competition.
The challenge of a machine learning competition can be framed as an optimization problem. Traditionally, the competition participant acts as the optimization algorithm, exploring different modeling pipelines that result in different sets of predictions, scoring the predictions, then making changes to the pipeline that are expected to result in an improved score.
This process can also be modeled directly with an optimization algorithm where candidate predictions are generated and evaluated without ever looking at the test set.
Generally, this is referred to as hill climbing the test set, as one of the simplest optimization algorithms to implement to solve this problem is the hill climbing algorithm.
Although hill climbing the test set is rightfully frowned upon in actual machine learning competitions, it can be an interesting exercise to implement the approach in order to learn about the limitations of the approach and the dangers of overfitting the test set. Additionally, the fact that the test set can be predicted perfectly without ever touching the training dataset often shocks a lot of beginner machine learning practitioners.
Most importantly, we implicitly hill climb the test set when we repeatedly evaluate different modeling pipelines. The risk is that score is improved on the test set at the cost of increased generalization error, i.e. worse performance on the broader problem.
People that run machine learning competitions are well aware of this problem and impose limitations on prediction evaluation to counter it, such as limiting evaluation to one or a few per day and reporting scores on a hidden subset of the test set rather than the entire test set. For more on this, see the papers listed in the further reading section.
Next, let’s look at how we can implement the hill climbing algorithm to optimize predictions for a test set.
Want to Get Started With Data Preparation?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Hill Climbing Algorithm
The hill climbing algorithm is a very simple optimization algorithm.
It involves generating a candidate solution and evaluating it. This is the starting point that is then incrementally improved until either no further improvement can be achieved or we run out of time, resources, or interest.
New candidate solutions are generated from the existing candidate solution. Typically, this involves making a single change to the candidate solution, evaluating it, and accepting the candidate solution as the new “current” solution if it is as good or better than the previous current solution. Otherwise, it is discarded.
We might think that it is a good idea to accept only candidates that have a better score. This is a reasonable approach for many simple problems, although, on more complex problems, it is desirable to accept different candidates with the same score in order to aid the search process to scale flat areas (plateaus) in the feature space.
When hill climbing the test set, a candidate solution is a list of predictions. For a binary classification task, this is a list of 0 and 1 values for the two classes. For a regression task, this is a list of numbers in the range of the target variable.
A modification to a candidate solution for classification would be to select one prediction and flip it from 0 to 1 or 1 to 0. A modification to a candidate solution for regression would be to add Gaussian noise to one value in the list or replace a value in the list with a new value.
Scoring of solutions involves calculating a scoring metric, such as classification accuracy on classification tasks or mean absolute error for a regression task.
Now that we are familiar with the algorithm, let’s implement it.
How to Implement Hill Climbing
We will develop our hill climbing algorithm on a synthetic classification task.
First, let’s create a binary classification task with many input variables and 5,000 rows of examples. We can then split the dataset into train and test sets.
The complete example is listed below.
# example of a synthetic dataset. from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split # define dataset X, y = make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1) print(X.shape, y.shape) # split dataset X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
Running the example first reports the shape of the created dataset, showing 5,000 rows and 20 input variables.
The dataset is then split into train and test sets with about 3,300 for training and about 1,600 for testing.
(5000, 20) (5000,) (3350, 20) (1650, 20) (3350,) (1650,)
Now we can develop a hill climber.
First, we can create a function that will load, or in this case, define the dataset. We can update this function later when we want to change the dataset.
# load or prepare the classification dataset def load_dataset(): return make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
Next, we need a function to evaluate candidate solutions–that is, lists of predictions.
We will use classification accuracy where scores range between 0 for the worst possible solution to 1 for a perfect set of predictions.
# evaluate a set of predictions def evaluate_predictions(y_test, yhat): return accuracy_score(y_test, yhat)
Next, we need a function to create an initial candidate solution.
That is a list of predictions for 0 and 1 class labels, long enough to match the number of examples in the test set, in this case, 1650.
We can use the randint() function to generate random values of 0 and 1.
# create a random set of predictions def random_predictions(n_examples): return [randint(0, 1) for _ in range(n_examples)]
Next, we need a function to create a modified version of a candidate solution.
In this case, this involves selecting one value in the solution and flipping it from 0 to 1 or 1 to 0.
Typically, we make a single change for each new candidate solution during hill climbing, but I have parameterized the function so you can explore making more than one change if you want.
# modify the current set of predictions def modify_predictions(current, n_changes=1): # copy current solution updated = current.copy() for i in range(n_changes): # select a point to change ix = randint(0, len(updated)-1) # flip the class label updated[ix] = 1 - updated[ix] return updated
So far, so good.
Next, we can develop the function that performs the search.
First, an initial solution is created and evaluated by calling the random_predictions() function followed by the evaluate_predictions() function.
Then we loop for a fixed number of iterations and generate a new candidate by calling modify_predictions(), evaluate it, and if the score is as good as or better than the current solution, replace it.
The loop ends when we finish the pre-set number of iterations (chosen arbitrarily) or when a perfect score is achieved, which we know in this case is an accuracy of 1.0 (100 percent).
The function hill_climb_testset() below implements this, taking the test set as input and returning the best set of predictions found during the hill climbing.
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
scores = list()
# generate the initial solution
solution = random_predictions(X_test.shape[0])
# evaluate the initial solution
score = evaluate_predictions(y_test, solution)
scores.append(score)
# hill climb to a solution
for i in range(max_iterations):
# record scores
scores.append(score)
# stop once we achieve the best score
if score == 1.0:
break
# generate new candidate
candidate = modify_predictions(solution)
# evaluate candidate
value = evaluate_predictions(y_test, candidate)
# check if it is as good or better
if value >= score:
solution, score = candidate, value
print('>%d, score=%.3f' % (i, score))
return solution, scores
That’s all there is to it.
The complete example of hill climbing the test set is listed below.
# example of hill climbing the test set for a classification task
from random import randint
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib import pyplot
# load or prepare the classification dataset
def load_dataset():
return make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
return accuracy_score(y_test, yhat)
# create a random set of predictions
def random_predictions(n_examples):
return [randint(0, 1) for _ in range(n_examples)]
# modify the current set of predictions
def modify_predictions(current, n_changes=1):
# copy current solution
updated = current.copy()
for i in range(n_changes):
# select a point to change
ix = randint(0, len(updated)-1)
# flip the class label
updated[ix] = 1 - updated[ix]
return updated
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
scores = list()
# generate the initial solution
solution = random_predictions(X_test.shape[0])
# evaluate the initial solution
score = evaluate_predictions(y_test, solution)
scores.append(score)
# hill climb to a solution
for i in range(max_iterations):
# record scores
scores.append(score)
# stop once we achieve the best score
if score == 1.0:
break
# generate new candidate
candidate = modify_predictions(solution)
# evaluate candidate
value = evaluate_predictions(y_test, candidate)
# check if it is as good or better
if value >= score:
solution, score = candidate, value
print('>%d, score=%.3f' % (i, score))
return solution, scores
# load the dataset
X, y = load_dataset()
print(X.shape, y.shape)
# split dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# run hill climb
yhat, scores = hill_climb_testset(X_test, y_test, 20000)
# plot the scores vs iterations
pyplot.plot(scores)
pyplot.show()
Running the example will run the search for 20,000 iterations or stop if a perfect accuracy is achieved.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we found a perfect set of predictions for the test set in about 12,900 iterations.
Recall that this was achieved without touching the training dataset and without cheating by looking at the test set target values. Instead, we simply optimized a set of numbers.
The lesson here is that repeated evaluation of a modeling pipeline against a test set will do the same thing, using you as the hill climbing optimization algorithm. The solution will be overfit to the test set.
... >8092, score=0.996 >8886, score=0.997 >9202, score=0.998 >9322, score=0.998 >9521, score=0.999 >11046, score=0.999 >12932, score=1.000
A plot is also created of the progress of the optimization.
This can be helpful to see how changes to the optimization algorithm, such as the choice of what to change and how it is changed during the hill climb, impact the convergence of the search.
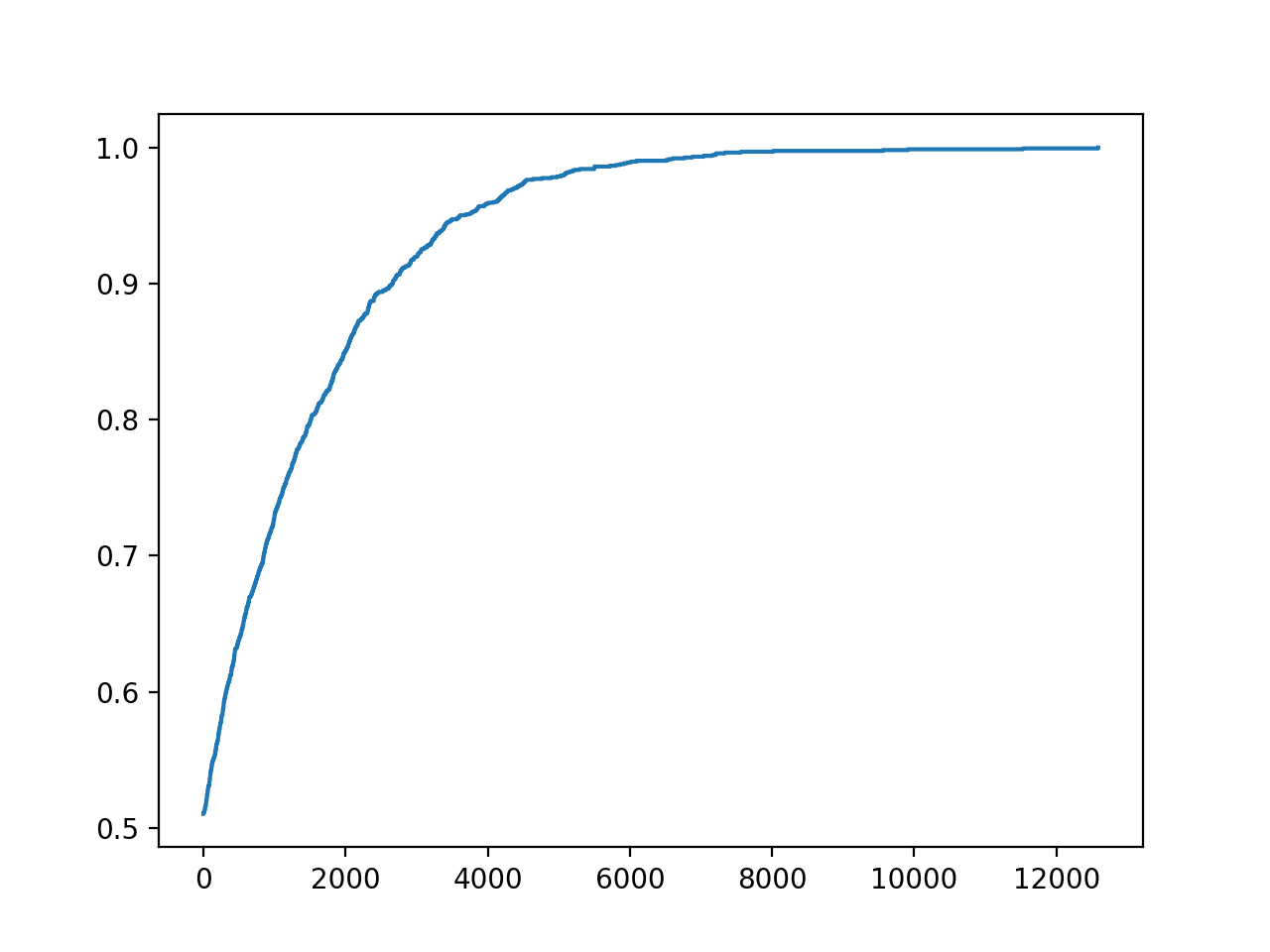
Line Plot of Accuracy vs. Hill Climb Optimization Iteration for a Classification Task
Now that we are familiar with hill climbing the test set, let’s try the approach on a real dataset.
Hill Climb Diabetes Classification Dataset
We will use the diabetes dataset as the basis for exploring hill climbing the test set for a classification problem.
Each record describes the medical details of a female, and the prediction is the onset of diabetes within the next five years.
The dataset has eight input variables and 768 rows of data; the input variables are all numeric and the target has two class labels, e.g. it is a binary classification task.
Below provides a sample of the first five rows of the dataset.
6,148,72,35,0,33.6,0.627,50,1 1,85,66,29,0,26.6,0.351,31,0 8,183,64,0,0,23.3,0.672,32,1 1,89,66,23,94,28.1,0.167,21,0 0,137,40,35,168,43.1,2.288,33,1 ...
We can load the dataset directly using Pandas, as follows.
# load or prepare the classification dataset def load_dataset(): url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv' df = read_csv(url, header=None) data = df.values return data[:, :-1], data[:, -1]
The rest of the code remains unchanged.
This is created so that you can drop in your own binary classification task and try it out.
The complete example is listed below.
# example of hill climbing the test set for the diabetes dataset
from random import randint
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib import pyplot
# load or prepare the classification dataset
def load_dataset():
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv'
df = read_csv(url, header=None)
data = df.values
return data[:, :-1], data[:, -1]
# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
return accuracy_score(y_test, yhat)
# create a random set of predictions
def random_predictions(n_examples):
return [randint(0, 1) for _ in range(n_examples)]
# modify the current set of predictions
def modify_predictions(current, n_changes=1):
# copy current solution
updated = current.copy()
for i in range(n_changes):
# select a point to change
ix = randint(0, len(updated)-1)
# flip the class label
updated[ix] = 1 - updated[ix]
return updated
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
scores = list()
# generate the initial solution
solution = random_predictions(X_test.shape[0])
# evaluate the initial solution
score = evaluate_predictions(y_test, solution)
scores.append(score)
# hill climb to a solution
for i in range(max_iterations):
# record scores
scores.append(score)
# stop once we achieve the best score
if score == 1.0:
break
# generate new candidate
candidate = modify_predictions(solution)
# evaluate candidate
value = evaluate_predictions(y_test, candidate)
# check if it is as good or better
if value >= score:
solution, score = candidate, value
print('>%d, score=%.3f' % (i, score))
return solution, scores
# load the dataset
X, y = load_dataset()
print(X.shape, y.shape)
# split dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# run hill climb
yhat, scores = hill_climb_testset(X_test, y_test, 5000)
# plot the scores vs iterations
pyplot.plot(scores)
pyplot.show()
Running the example reports the iteration number and accuracy each time an improvement is seen during the search.
We use fewer iterations in this case because it is a simpler problem to optimize as we have fewer predictions to make.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that we achieved perfect accuracy in about 1,500 iterations.
... >617, score=0.961 >627, score=0.965 >650, score=0.969 >683, score=0.972 >743, score=0.976 >803, score=0.980 >817, score=0.984 >945, score=0.988 >1350, score=0.992 >1387, score=0.996 >1565, score=1.000
A line plot of the search progress is also created showing that convergence was rapid.
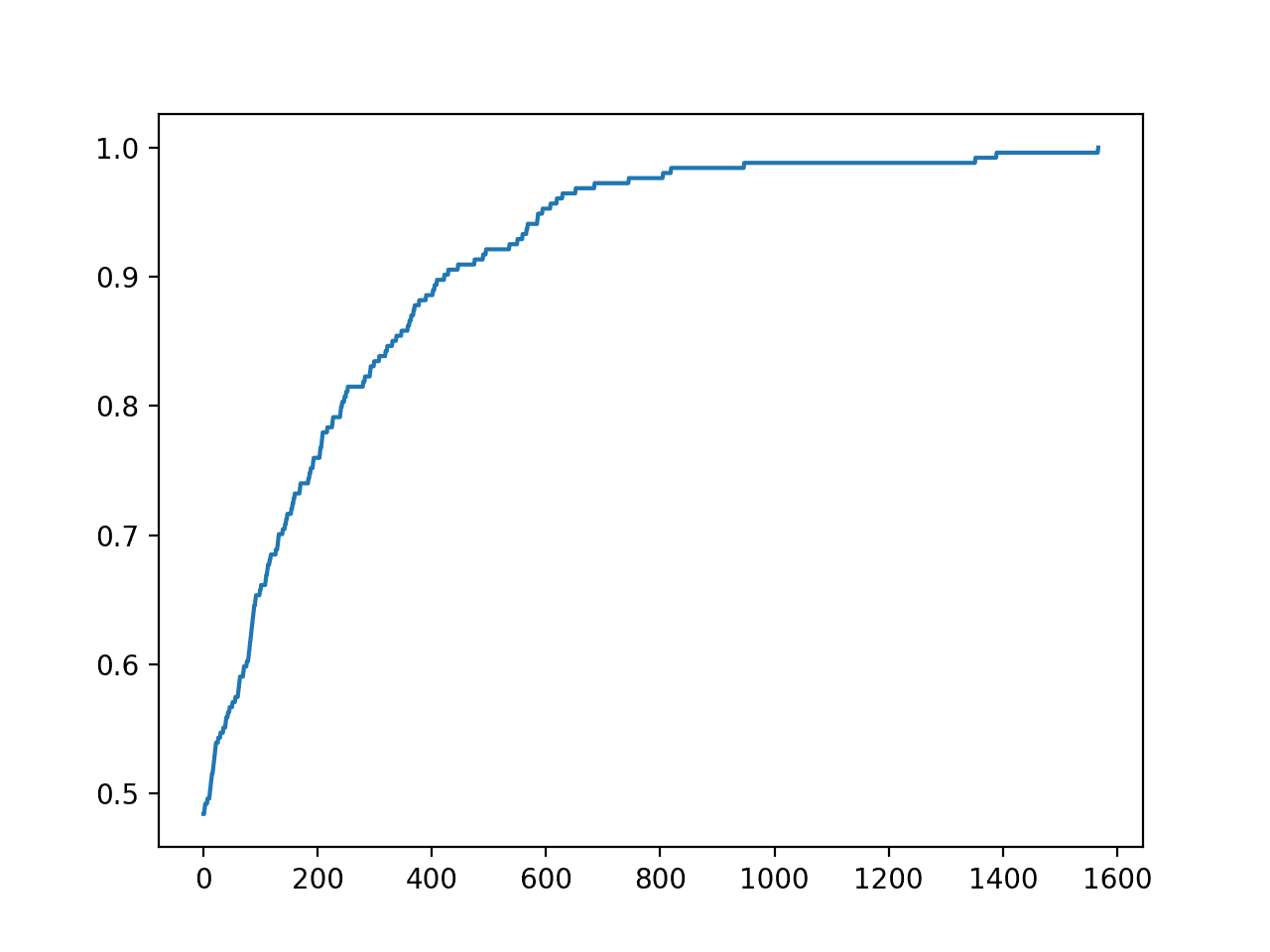
Line Plot of Accuracy vs. Hill Climb Optimization Iteration for the Diabetes Dataset
Hill Climb Housing Regression Dataset
We will use the housing dataset as the basis for exploring hill climbing the test set regression problem.
The housing dataset involves the prediction of a house price in thousands of dollars given details of the house and its neighborhood.
It is a regression problem, meaning we are predicting a numerical value. There are 506 observations with 13 input variables and one output variable.
A sample of the first five rows is listed below.
0.00632,18.00,2.310,0,0.5380,6.5750,65.20,4.0900,1,296.0,15.30,396.90,4.98,24.00 0.02731,0.00,7.070,0,0.4690,6.4210,78.90,4.9671,2,242.0,17.80,396.90,9.14,21.60 0.02729,0.00,7.070,0,0.4690,7.1850,61.10,4.9671,2,242.0,17.80,392.83,4.03,34.70 0.03237,0.00,2.180,0,0.4580,6.9980,45.80,6.0622,3,222.0,18.70,394.63,2.94,33.40 0.06905,0.00,2.180,0,0.4580,7.1470,54.20,6.0622,3,222.0,18.70,396.90,5.33,36.20 ...
First, we can update the load_dataset() function to load the housing dataset.
As part of loading the dataset, we will normalize the target value. This will make hill climbing the predictions simpler as we can limit the floating-point values to range 0 to 1.
This is not required generally, just the approach taken here to simplify the search algorithm.
# load or prepare the classification dataset def load_dataset(): url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' df = read_csv(url, header=None) data = df.values X, y = data[:, :-1], data[:, -1] # normalize the target scaler = MinMaxScaler() y = y.reshape((len(y), 1)) y = scaler.fit_transform(y) return X, y
Next, we can update the scoring function to use the mean absolute error between the expected and predicted values.
# evaluate a set of predictions def evaluate_predictions(y_test, yhat): return mean_absolute_error(y_test, yhat)
We must also update the representation for a solution from 0 and 1 labels to floating-point values between 0 and 1.
The generation of the initial candidate solution must be changed to create a list of random floats.
# create a random set of predictions def random_predictions(n_examples): return [random() for _ in range(n_examples)]
The single change made to a solution to create a new candidate solution, in this case, involves simply replacing a randomly chosen prediction in the list with a new random float.
I chose this because it was simple.
# modify the current set of predictions def modify_predictions(current, n_changes=1): # copy current solution updated = current.copy() for i in range(n_changes): # select a point to change ix = randint(0, len(updated)-1) # flip the class label updated[ix] = random() return updated
A better approach would be to add Gaussian noise to an existing value, and I leave this to you as an extension. If you try it, let me know in the comments below.
For example:
... # add gaussian noise updated[ix] += gauss(0, 0.1)
Finally, the search must be updated.
The best value is now an error of 0.0, used to stop the search if found.
... # stop once we achieve the best score if score == 0.0: break
We also need to change the search from maximizing the score to now minimize the score.
...
# check if it is as good or better
if value <= score:
solution, score = candidate, value
print('>%d, score=%.3f' % (i, score))
The updated search function with both of these changes is listed below.
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
scores = list()
# generate the initial solution
solution = random_predictions(X_test.shape[0])
# evaluate the initial solution
score = evaluate_predictions(y_test, solution)
print('>%.3f' % score)
# hill climb to a solution
for i in range(max_iterations):
# record scores
scores.append(score)
# stop once we achieve the best score
if score == 0.0:
break
# generate new candidate
candidate = modify_predictions(solution)
# evaluate candidate
value = evaluate_predictions(y_test, candidate)
# check if it is as good or better
if value <= score:
solution, score = candidate, value
print('>%d, score=%.3f' % (i, score))
return solution, scores
Tying this together, the complete example of hill climbing the test set for a regression task is listed below.
# example of hill climbing the test set for the housing dataset
from random import random
from random import randint
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot
# load or prepare the classification dataset
def load_dataset():
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
df = read_csv(url, header=None)
data = df.values
X, y = data[:, :-1], data[:, -1]
# normalize the target
scaler = MinMaxScaler()
y = y.reshape((len(y), 1))
y = scaler.fit_transform(y)
return X, y
# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
return mean_absolute_error(y_test, yhat)
# create a random set of predictions
def random_predictions(n_examples):
return [random() for _ in range(n_examples)]
# modify the current set of predictions
def modify_predictions(current, n_changes=1):
# copy current solution
updated = current.copy()
for i in range(n_changes):
# select a point to change
ix = randint(0, len(updated)-1)
# flip the class label
updated[ix] = random()
return updated
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
scores = list()
# generate the initial solution
solution = random_predictions(X_test.shape[0])
# evaluate the initial solution
score = evaluate_predictions(y_test, solution)
print('>%.3f' % score)
# hill climb to a solution
for i in range(max_iterations):
# record scores
scores.append(score)
# stop once we achieve the best score
if score == 0.0:
break
# generate new candidate
candidate = modify_predictions(solution)
# evaluate candidate
value = evaluate_predictions(y_test, candidate)
# check if it is as good or better
if value <= score:
solution, score = candidate, value
print('>%d, score=%.3f' % (i, score))
return solution, scores
# load the dataset
X, y = load_dataset()
print(X.shape, y.shape)
# split dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# run hill climb
yhat, scores = hill_climb_testset(X_test, y_test, 100000)
# plot the scores vs iterations
pyplot.plot(scores)
pyplot.show()
Running the example reports the iteration number and MAE each time an improvement is seen during the search.
We use many more iterations in this case because it is a more complex problem to optimize. The chosen method for creating candidate solutions also makes it slower and less likely we will achieve perfect error.
In fact, we would not achieve perfect error; instead, it would be better to stop if error reached a value below a minimum value such as 1e-7 or something meaningful to the target domain. This, too, is left as an exercise for the reader.
For example:
... # stop once we achieve a good enough if score <= 1e-7: break
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that we achieved a good error by the end of the run.
... >95991, score=0.001 >96011, score=0.001 >96295, score=0.001 >96366, score=0.001 >96585, score=0.001 >97575, score=0.001 >98828, score=0.001 >98947, score=0.001 >99712, score=0.001 >99913, score=0.001
A line plot of the search progress is also created showing that convergence was rapid and sits flat for most of the iterations.
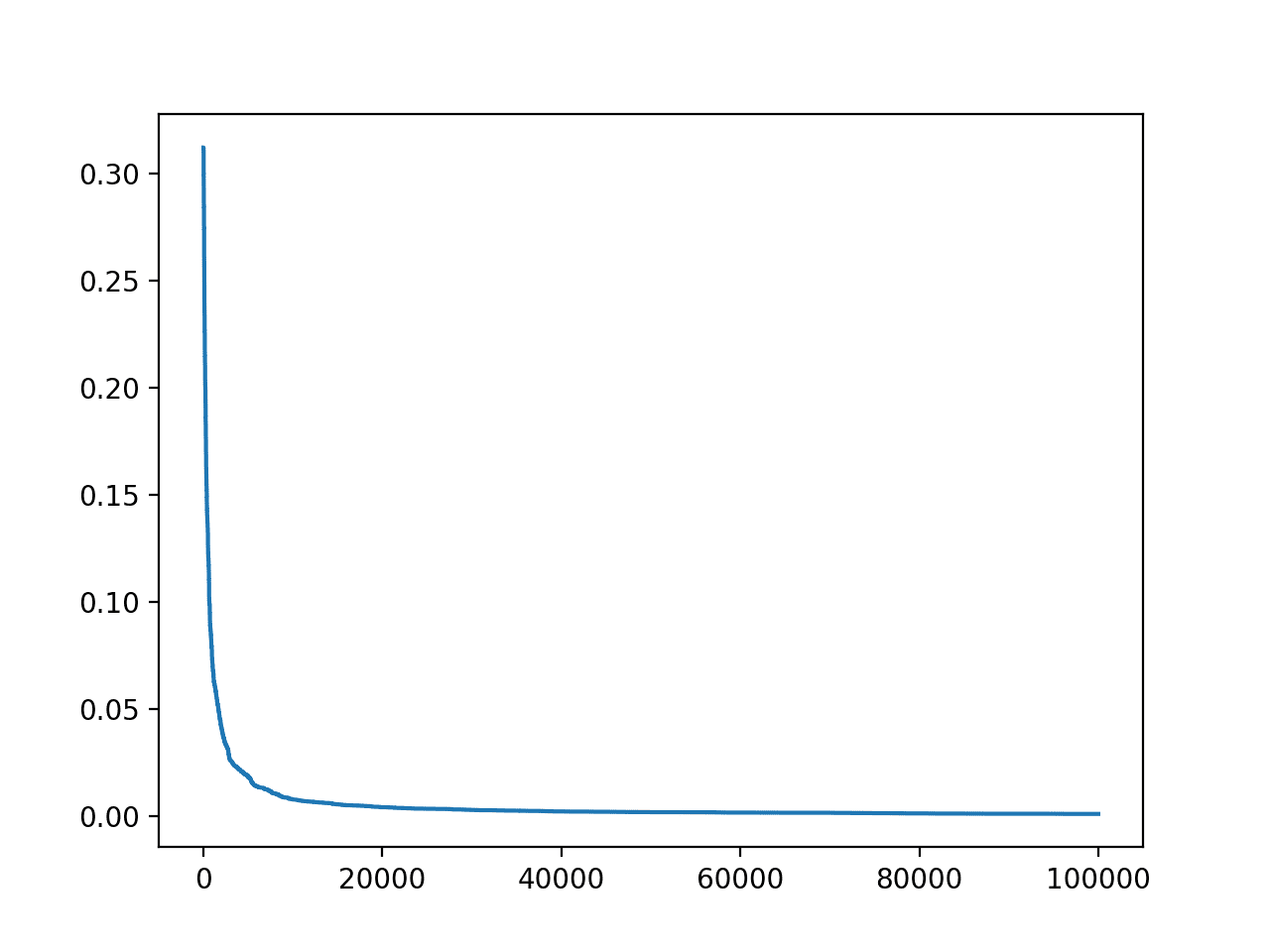
Line Plot of Accuracy vs. Hill Climb Optimization Iteration for the Housing Dataset
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
- Climbing the Kaggle Leaderboard by Exploiting the Log-Loss Oracle, 2018.
- Toward a Better Understanding of Leaderboard, 2017.
- The Ladder: A Reliable Leaderboard for Machine Learning Competitions, 2015.
Articles
Summary
In this tutorial, you discovered how to hill climb the test set for machine learning.
Specifically, you learned:
- Perfect predictions can be made by hill climbing the test set without even looking at the training dataset.
- How to hill climb the test set for classification and regression tasks.
- We implicitly hill climb the test set when we overuse the test set to evaluate our modeling pipelines.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post How to Hill Climb the Test Set for Machine Learning appeared first on Machine Learning Mastery.
