Author: Adrian Tam
Vector space models are to consider the relationship between data that are represented by vectors. It is popular in information retrieval systems but also useful for other purposes. Generally, this allows us to compare the similarity of two vectors from a geometric perspective.
In this tutorial, we will see what is a vector space model and what it can do.
After completing this tutorial, you will know:
- What is a vector space model and the properties of cosine similarity
- How cosine similarity can help you compare two vectors
- What is the difference between cosine similarity and L2 distance
Let’s get started.

A Gentle Introduction to Vector Space Models
Photo by liamfletch, some rights reserved.
Tutorial overview
This tutorial is divided into 3 parts; they are:
- Vector space and cosine formula
- Using vector space model for similarity
- Common use of vector space models and cosine distance
Vector space and cosine formula
A vector space is a mathematical term that defines some vector operations. In layman’s term, we can imagine it is a $n$-dimensional metric space where each point is represented by a $n$-dimensional vector. In this space, we can do any vector addition or scalar-vector multiplications.
It is useful to consider a vector space because it is useful to represent things as a vector. For example in machine learning, we usually have a data point with multiple features. Therefore, it is convenient for us to represent a data point as a vector.
With a vector, we can compute its norm. The most common one is the L2-norm or the length of the vector. With two vectors in the same vector space, we can find their difference. Assume it is a 3-dimensional vector space, the two vectors are $(x_1, x_2, x_3)$ and $(y_1, y_2, y_3)$. Their difference is the vector $(y_1-x_1, y_2-x_2, y_3-x_3)$, and the L2-norm of the difference is the distance or more precisely the Euclidean distance between those two vectors:
$$
sqrt{(y_1-x_1)^2+(y_2-x_2)^2+(y_3-x_3)^2}
$$
Besides distance, we can also consider the angle between two vectors. If we consider the vector $(x_1, x_2, x_3)$ as a line segment from the point $(0,0,0)$ to $(x_1,x_2,x_3)$ in the 3D coordinate system, then there is another line segment from $(0,0,0)$ to $(y_1,y_2, y_3)$. They make an angle at their intersection:
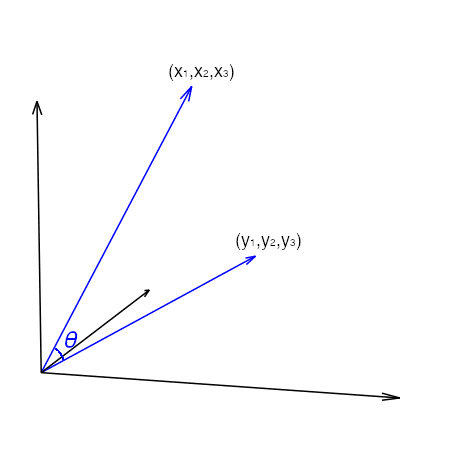
The angle between the two line segments can be found using the cosine formula:
$$
cos theta = frac{acdot b} {lVert arVert_2lVert brVert_2}
$$
where $acdot b$ is the vector dot-product and $lVert arVert_2$ is the L2-norm of vector $a$. This formula arises from considering the dot-product as the projection of vector $a$ onto the direction as pointed by vector $b$. The nature of cosine tells that, as the angle $theta$ increases from 0 to 90 degrees, cosine decreases from 1 to 0. Sometimes we would call $1-costheta$ the cosine distance because it runs from 0 to 1 as the two vectors are moving further away from each other. This is an important property that we are going to exploit in the vector space model.
Using vector space model for similarity
Let’s look at an example of how the vector space model is useful.
World Bank collects various data about countries and regions in the world. While every country is different, we can try to compare countries under vector space model. For convenience, we will use the pandas_datareader module in Python to read data from World Bank. You may install pandas_datareader using pip or conda command:
pip install pandas_datareader
The data series collected by World Bank are named by an identifier. For example, “SP.URB.TOTL” is the total urban population of a country. Many of the series are yearly. When we download a series, we have to put in the start and end years. Usually the data are not updated on time. Hence it is best to look at the data a few years back rather than the most recent year to avoid missing data.
In below, we try to collect some economic data of every country in 2010:
from pandas_datareader import wb
import pandas as pd
pd.options.display.width = 0
names = [
"NE.EXP.GNFS.CD", # Exports of goods and services (current US$)
"NE.IMP.GNFS.CD", # Imports of goods and services (current US$)
"NV.AGR.TOTL.CD", # Agriculture, forestry, and fishing, value added (current US$)
"NY.GDP.MKTP.CD", # GDP (current US$)
"NE.RSB.GNFS.CD", # External balance on goods and services (current US$)
]
df = wb.download(country="all", indicator=names, start=2010, end=2010).reset_index()
countries = wb.get_countries()
non_aggregates = countries[countries["region"] != "Aggregates"].name
df_nonagg = df[df["country"].isin(non_aggregates)].dropna()
print(df_nonagg)
country year NE.EXP.GNFS.CD NE.IMP.GNFS.CD NV.AGR.TOTL.CD NY.GDP.MKTP.CD NE.RSB.GNFS.CD 50 Albania 2010 3.337089e+09 5.792189e+09 2.141580e+09 1.192693e+10 -2.455100e+09 51 Algeria 2010 6.197541e+10 5.065473e+10 1.364852e+10 1.612073e+11 1.132067e+10 54 Angola 2010 5.157282e+10 3.568226e+10 5.179055e+09 8.379950e+10 1.589056e+10 55 Antigua and Barbuda 2010 9.142222e+08 8.415185e+08 1.876296e+07 1.148700e+09 7.270370e+07 56 Argentina 2010 8.020887e+10 6.793793e+10 3.021382e+10 4.236274e+11 1.227093e+10 .. ... ... ... ... ... ... ... 259 Venezuela, RB 2010 1.121794e+11 6.922736e+10 2.113513e+10 3.931924e+11 4.295202e+10 260 Vietnam 2010 8.347359e+10 9.299467e+10 2.130649e+10 1.159317e+11 -9.521076e+09 262 West Bank and Gaza 2010 1.367300e+09 5.264300e+09 8.716000e+08 9.681500e+09 -3.897000e+09 264 Zambia 2010 7.503513e+09 6.256989e+09 1.909207e+09 2.026556e+10 1.246524e+09 265 Zimbabwe 2010 3.569254e+09 6.440274e+09 1.157187e+09 1.204166e+10 -2.871020e+09 [174 rows x 7 columns]
In the above we obtained some economic metrics of each country in 2010. The function wb.download() will download the data from World Bank and return a pandas dataframe. Similarly wb.get_countries() will get the name of the countries and regions as identified by World Bank, which we will use this to filter out the non-countries aggregates such as “East Asia” and “World”. Pandas allows filtering rows by boolean indexing, which df["country"].isin(non_aggregates) gives a boolean vector of which row is in the list of non_aggregates and based on that, df[df["country"].isin(non_aggregates)] selects only those. For various reasons not all countries will have all data. Hence we use dropna() to remove those with missing data. In practice, we may want to apply some imputation techniques instead of merely removing them. But as an example, we proceed with the 174 remaining data points.
To better illustrate the idea rather than hiding the actual manipulation in pandas or numpy functions, we first extract the data for each country as a vector:
...
vectors = {}
for rowid, row in df_nonagg.iterrows():
vectors[row["country"]] = row[names].values
print(vectors)
{'Albania': array([3337088824.25553, 5792188899.58985, 2141580308.0144,
11926928505.5231, -2455100075.33431], dtype=object),
'Algeria': array([61975405318.205, 50654732073.2396, 13648522571.4516,
161207310515.42, 11320673244.9655], dtype=object),
'Angola': array([51572818660.8665, 35682259098.1843, 5179054574.41704,
83799496611.2004, 15890559562.6822], dtype=object),
...
'West Bank and Gaza': array([1367300000.0, 5264300000.0, 871600000.0, 9681500000.0,
-3897000000.0], dtype=object),
'Zambia': array([7503512538.82554, 6256988597.27752, 1909207437.82702,
20265559483.8548, 1246523941.54802], dtype=object),
'Zimbabwe': array([3569254400.0, 6440274000.0, 1157186600.0, 12041655200.0,
-2871019600.0], dtype=object)}
The Python dictionary we created has the name of each country as a key and the economic metrics as a numpy array. There are 5 metrics, hence each is a vector of 5 dimensions.
What this helps us is that, we can use the vector representation of each country to see how similar it is to another. Let’s try both the L2-norm of the difference (the Euclidean distance) and the cosine distance. We pick one country, such as Australia, and compare it to all other countries on the list based on the selected economic metrics.
...
import numpy as np
euclid = {}
cosine = {}
target = "Australia"
for country in vectors:
vecA = vectors[target]
vecB = vectors[country]
dist = np.linalg.norm(vecA - vecB)
cos = (vecA @ vecB) / (np.linalg.norm(vecA) * np.linalg.norm(vecB))
euclid[country] = dist # Euclidean distance
cosine[country] = 1-cos # cosine distance
In the for-loop above, we set vecA as the vector of the target country (i.e., Australia) and vecB as that of the other country. Then we compute the L2-norm of their difference as the Euclidean distance between the two vectors. We also compute the cosine similarity using the formula and minus it from 1 to get the cosine distance. With more than a hundred countries, we can see which one has the shortest Euclidean distance to Australia:
...
import pandas as pd
df_distance = pd.DataFrame({"euclid": euclid, "cos": cosine})
print(df_distance.sort_values(by="euclid").head())
euclid cos Australia 0.000000e+00 -2.220446e-16 Mexico 1.533802e+11 7.949549e-03 Spain 3.411901e+11 3.057903e-03 Turkey 3.798221e+11 3.502849e-03 Indonesia 4.083531e+11 7.417614e-03
By sorting the result, we can see that Mexico is the closest to Australia under Euclidean distance. However, with cosine distance, it is Colombia the closest to Australia.
... df_distance.sort_values(by="cos").head()
euclid cos Australia 0.000000e+00 -2.220446e-16 Colombia 8.981118e+11 1.720644e-03 Cuba 1.126039e+12 2.483993e-03 Italy 1.088369e+12 2.677707e-03 Argentina 7.572323e+11 2.930187e-03
To understand why the two distances give different result, we can observe how the three countries’ metric compare to each other:
... print(df_nonagg[df_nonagg.country.isin(["Mexico", "Colombia", "Australia"])])
country year NE.EXP.GNFS.CD NE.IMP.GNFS.CD NV.AGR.TOTL.CD NY.GDP.MKTP.CD NE.RSB.GNFS.CD 59 Australia 2010 2.270501e+11 2.388514e+11 2.518718e+10 1.146138e+12 -1.180129e+10 91 Colombia 2010 4.682683e+10 5.136288e+10 1.812470e+10 2.865631e+11 -4.536047e+09 176 Mexico 2010 3.141423e+11 3.285812e+11 3.405226e+10 1.057801e+12 -1.443887e+10
From this table, we see that the metrics of Australia and Mexico are very close to each other in magnitude. However, if you compare the ratio of each metric within the same country, it is Colombia that match Australia better. In fact from the cosine formula, we can see that
$$
cos theta = frac{acdot b} {lVert arVert_2lVert brVert_2} = frac{a}{lVert arVert_2} cdot frac{b} {lVert brVert_2}
$$
which means the cosine of the angle between the two vector is the dot-product of the corresponding vectors after they were normalized to length of 1. Hence cosine distance is virtually applying a scaler to the data before computing the distance.
Putting these altogether, the following is the complete code
from pandas_datareader import wb
import numpy as np
import pandas as pd
pd.options.display.width = 0
# Download data from World Bank
names = [
"NE.EXP.GNFS.CD", # Exports of goods and services (current US$)
"NE.IMP.GNFS.CD", # Imports of goods and services (current US$)
"NV.AGR.TOTL.CD", # Agriculture, forestry, and fishing, value added (current US$)
"NY.GDP.MKTP.CD", # GDP (current US$)
"NE.RSB.GNFS.CD", # External balance on goods and services (current US$)
]
df = wb.download(country="all", indicator=names, start=2010, end=2010).reset_index()
# We remove aggregates and keep only countries with no missing data
countries = wb.get_countries()
non_aggregates = countries[countries["region"] != "Aggregates"].name
df_nonagg = df[df["country"].isin(non_aggregates)].dropna()
# Extract vector for each country
vectors = {}
for rowid, row in df_nonagg.iterrows():
vectors[row["country"]] = row[names].values
# Compute the Euclidean and cosine distances
euclid = {}
cosine = {}
target = "Australia"
for country in vectors:
vecA = vectors[target]
vecB = vectors[country]
dist = np.linalg.norm(vecA - vecB)
cos = (vecA @ vecB) / (np.linalg.norm(vecA) * np.linalg.norm(vecB))
euclid[country] = dist # Euclidean distance
cosine[country] = 1-cos # cosine distance
# Print the results
df_distance = pd.DataFrame({"euclid": euclid, "cos": cosine})
print("Closest by Euclidean distance:")
print(df_distance.sort_values(by="euclid").head())
print()
print("Closest by Cosine distance:")
print(df_distance.sort_values(by="cos").head())
# Print the detail metrics
print()
print("Detail metrics:")
print(df_nonagg[df_nonagg.country.isin(["Mexico", "Colombia", "Australia"])])
Common use of vector space models and cosine distance
Vector space models are common in information retrieval systems. We can present documents (e.g., a paragraph, a long passage, a book, or even a sentence) as vectors. This vector can be as simple as counting of the words that the document contains (i.e., a bag-of-word model) or a complicated embedding vector (e.g., Doc2Vec). Then a query to find the most relevant document can be answered by ranking all documents by the cosine distance. Cosine distance should be used because we do not want to favor longer or shorter documents, but to focus on what it contains. Hence we leverage the normalization comes with it to consider how relevant are the documents to the query rather than how many times the words on the query are mentioned in a document.
If we consider each word in a document as a feature and compute the cosine distance, it is the “hard” distance because we do not care about words with similar meanings (e.g. “document” and “passage” have similar meanings but not “distance”). Embedding vectors such as word2vec would allow us to consider the ontology. Computing the cosine distance with the meaning of words considered is the “soft cosine distance“. Libraries such as gensim provides a way to do this.
Another use case of the cosine distance and vector space model is in computer vision. Imagine the task of recognizing hand gesture, we can make certain parts of the hand (e.g. five fingers) the key points. Then with the (x,y) coordinates of the key points lay out as a vector, we can compare with our existing database to see which cosine distance is the closest and determine which hand gesture it is. We need cosine distance because everyone’s hand has a different size. We do not want that to affect our decision on what gesture it is showing.
As you may imagine, there are much more examples you can use this technique.
Further reading
This section provides more resources on the topic if you are looking to go deeper.
Books
- Introduction to Linear Algebra, Fifth Edition, 2016.
- Introduction to Information Retrieval, 2008.
Software
Articles
Summary
In this tutorial, you discovered the vector space model for measuring the similarities of vectors.
Specifically, you learned:
- How to construct a vector space model
- How to compute the cosine similarity and hence the cosine distance between two vectors in the vector space model
- How to interpret the difference between cosine distance and other distance metrics such as Euclidean distance
- What are the use of the vector space model
The post A Gentle Introduction to Vector Space Models appeared first on Machine Learning Mastery.
